题目内容
点（-3，b）与点（a+1，7）关于x轴对称，则点P（a，b）到原点的距离是
．
| 65 |
| 65 |
分析：根据点P（x，y）关于x轴对称的点的坐标为（x，-y）得到a+1=-3，b=-7，解得a=-4，b=-7，则点P坐标为（-4，-7），然后根据勾股定理计算出点P（a，b）到原点的距离．
解答：解：∵点（-3，b）与点（a+1，7）关于x轴对称，
∴a+1=-3，b=-7，
∴a=-4，b=-7，
∴点P坐标为（-4，-7），
∴点P（a，b）到原点的距离=
=
．
故答案为
．
∴a+1=-3，b=-7，
∴a=-4，b=-7，
∴点P坐标为（-4，-7），
∴点P（a，b）到原点的距离=
| 42+72 |
| 65 |
故答案为
| 65 |
点评：本题考查了关于x轴、y轴对称的点的坐标：点P（x，y）关于x轴对称的点的坐标为（x，-y），点P（x，y）关于y轴对称的点的坐标为（-x，y）．也考查了勾股定理．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
（2011•葫芦岛一模）如图，在矩形ABCD中，AD=8，AB=6，点M是BC的中点，点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动，在点P，Q的运动过程中，以PQ为边作正方形PQEF，使它与矩形ABCD在BC的同侧，点P，Q同时出发，当点P返回点M时停止运动，点Q也随之停止，设点P，Q运动的时间是t秒（t＞0）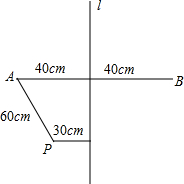
四跳落点于P4，P4与P3关于竹竿l成轴对称；以此跃下去，若每25跳可以休息一次．
，
；
，
，于是画出线段AB、AC、BC，从而画出格点△ABC.（1）请你参考小明同学的做法，在图2正方形网格（每个小正方形边长为1）中画出格点△
（
点位置如图所示），使
=
=5，
.（直接画出图形，不写过程）；
的形状，猜想∠BAC与∠
有怎样的数量关系，并证明你的猜想.
，
；
，
，于是画出线段AB、AC、BC，从而画出格点△ABC.（1）请你参考小明同学的做法，在图2正方形网格（每个小正方形边长为1）中画出格点△
（
点位置如图所示），使
=
=5，
.（直接画出图形，不写过程）；
的形状，猜想∠BAC与∠
