题目内容
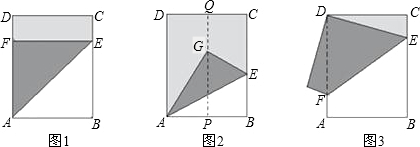
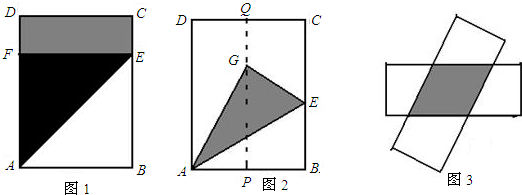
在一张长方形ABCD纸片中,AD=25cm,AB=20cm,现将这张纸片按下列图示方法折叠,请分别求折痕的长.(1)如图1,折痕为AE,点B的对应点F在AD上;
(2)如图2,P,Q分别为AB,CD的中点,B的对应点G在PQ上,折痕为AE;
(3)如图3,在图2中,把长方形ABCD沿着PQ对开,变成两张长方形纸片,将两张纸片任意叠合后,发现重叠部分是一个菱形,显然,这个菱形的周长最短是40cm,求叠合后周长最大的菱形的周长和面积.
分析:(1)根据有一组邻边相等的矩形,得四边形ABEF是正方形,根据勾股定理求得AE的长;
(2)根据折叠的性质,得AP=
AB=
AG,则∠GAP=60°,根据折叠的性质,则∠EAB=30°,从而根据解直角三角形的知识求得AE的长;
(3)最大的菱形显然是菱形的较长对角线和矩形的对角线重合的情况.根据勾股定理求得菱形的边长,进而求得菱形的周长和面积.
(2)根据折叠的性质,得AP=
| 1 |
| 2 |
| 1 |
| 2 |
(3)最大的菱形显然是菱形的较长对角线和矩形的对角线重合的情况.根据勾股定理求得菱形的边长,进而求得菱形的周长和面积.
解答:解:(1)∵四边形ABEF是正方形,
∴AE=20
;
(2)∵AP=
AB=
AG,
∴∠GAP=60°.
∵∠GAE=∠BAE,
∴∠EAB=30°.
∴AE=
=
=
;
(3)最大的菱形如图所示:
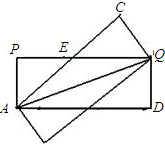
设QE=x,则PE=25-x.
x2=(25-x)2+102,
解得x=
.
则菱形的周长为58cm.
此时菱形的面积S=
×10=145.
∴AE=20
| 2 |
(2)∵AP=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GAP=60°.
∵∠GAE=∠BAE,
∴∠EAB=30°.
∴AE=
| AB |
| Cos30° |
| 20 | ||||
|
40
| ||
| 3 |
(3)最大的菱形如图所示:

设QE=x,则PE=25-x.
x2=(25-x)2+102,
解得x=
| 29 |
| 2 |
则菱形的周长为58cm.
此时菱形的面积S=
| 29 |
| 2 |
点评:此题综合运用了正方形的判定和性质、勾股定理、折叠的性质.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
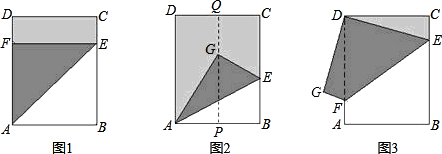
 如图,在一张长方形ABCD纸张中,一边BC折叠后落在对角线BD上,点E为折痕与边CD的交点,若AB=5,BC=12,求图中阴影部分的面积.
如图,在一张长方形ABCD纸张中,一边BC折叠后落在对角线BD上,点E为折痕与边CD的交点,若AB=5,BC=12,求图中阴影部分的面积.