Question

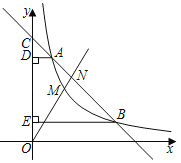
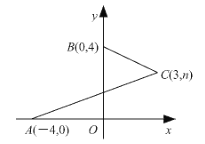
【题目】如图，在平面直角坐标系中，点、的坐标分别为、，点在第一象限内，连接、．已知，则_________．

Answer 1

【答案】

【解析】

过点C作CD⊥y轴，交y轴于点D，则CD∥AO，先证CDE≌CDB（ASA），进而可得DE＝DB＝4－n，再证AOE∽CDE，进而可得，由此计算即可求得答案．

解：如图，过点C作CD⊥y轴，交y轴于点D，则CD∥AO，

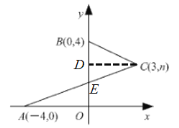
∴∠DCE＝∠CAO，

∵∠BCA＝2∠CAO，

∴∠BCA＝2∠DCE，

∴∠DCE＝∠DCB，

∵CD⊥y轴，

∴∠CDE＝∠CDB＝90°，

又∵CD＝CD，

∴CDE≌CDB（ASA），

∴DE＝DB，

∵B（0，4），C（3，n），

∴CD＝3，OD＝n，OB＝4，

∴DE＝DB＝OB－OD＝4－n，

∴OE＝OD－DE

＝n－（4－n）

＝2n－4，

∵A（－4，0），

∴AO＝4，

∵CD∥AO，

∴AOE∽CDE，

∴ ，

∴，

解得：，

故答案为：．