Question

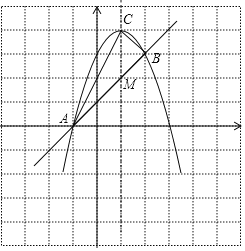
【题目】已知抛物线y1=ax2＋2x＋c与直线y2=kx＋b交于点A(－1，0)、B(2，3)．

（1）求a、b、c的值；

（2）直接写出当y1＜y2时，自变量的范围是__________________________．

（3）若点C是抛物线的顶点，求△ABC的面积．

Answer 1

【答案】

【解析】试题分析：（1）利用待定系数法即可求得；
（2）判断抛物线的开口，根据交点坐标即可求得；
（3）先利用配方法求出抛物线的顶点的坐标，设对称轴与直线交于点，求出 那么再根据 即可求解．

试题解析：(1)∵抛物线与直线交于点A(1,0)、B(2,3).

解得

∴a=1，b=1，c=3；

(2)

∴抛物线的开口向下，

∴x<1或x>2时，抛物线上的部分在直线的下方，

∴当y1<y2时，自变量的范围是x<1或x>2.

故答案为x<1或x>2；

(3)

∴抛物线的顶点C的坐标为(1,4).

设对称轴与直线交于点M，

∵当x=1时，y=1+1=2，

∴M(1,2)，

∴CM=42=2，

∵A(1,0),B(2,3)，