题目内容
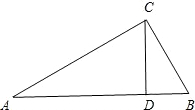如图，CD⊥AB，垂足为D，∠ACB=90°，∠A=30°，求证：BD=
AD．
证明：∵CD⊥AB，∠A=30°，
∴∠DCB=30°，
∴BC=2BD，
∵∠A=30°，∠ACB=90°，
∴AB=2BC，
∴AB=4BD，
∵AB=AD+BD，
∴AD=3BD，
∴BD=AD．
分析：根据直角三角形中30度所对的边是斜边的一半可得到BC=2BD，AB=2BC，从而可推出AB=4BD，从而不难证得BD与AD的数量关系．
点评：此题主要考查含30度角的直角三角形的性质：在直角三角形中，30°角所对的直角边等于斜边的一半．
∴∠DCB=30°，
∴BC=2BD，
∵∠A=30°，∠ACB=90°，
∴AB=2BC，
∴AB=4BD，
∵AB=AD+BD，
∴AD=3BD，
∴BD=
AD．分析：根据直角三角形中30度所对的边是斜边的一半可得到BC=2BD，AB=2BC，从而可推出AB=4BD，从而不难证得BD与AD的数量关系．
点评：此题主要考查含30度角的直角三角形的性质：在直角三角形中，30°角所对的直角边等于斜边的一半．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
如图，已知∠ACB=90°，CD⊥AB，垂点是D，∠BCD=55°，则∠A=