题目内容
如图所示，直线L1∥L2，C1，C2，C3是L1上的三点，连接C1A，C1B，C2A，C2B，C3A，C3B，得△C1AB，△C2AB，△C3AB，试说明△C1AB，△C2AB，△C3AB的面积相等．
解：底相同，高相等，则三个三角形的面积相等．
分析：根据两条平行线间的距离处处相等，再结合三角形的面积公式，可知：只要两个三角形是等底等高的，则两个三角形的面积相等．
点评：主要注意根据两条平行线间的距离的概念可知：夹在两条平行线间的距离处处相等．
分析：根据两条平行线间的距离处处相等，再结合三角形的面积公式，可知：只要两个三角形是等底等高的，则两个三角形的面积相等．
点评：主要注意根据两条平行线间的距离的概念可知：夹在两条平行线间的距离处处相等．
练习册系列答案
相关题目
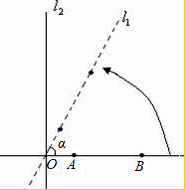如图所示，直线L1⊥L2，垂足为点O，A，B是直线L1上的两点，且OB=2，AB=
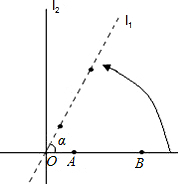角形，请用不等式表示α的取值范围：
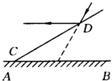44、如图所示，直线L1∥L2，C1，C2，C3是L1上的三点，连接C1A，C1B，C2A，C2B，C3A，C3B，得△C1AB，△C2AB，△C3AB，试说明△C1AB，△C2AB，△C3AB的面积相等．
2、如图所示，直线l1∥l2，∠1=40°，则∠2为（ ）