题目内容
如图，⊙O的半径OC=5cm，直线L⊥OC，垂足为H，且L交⊙O于A，B两点，AB=8cm，则L沿OC所在直线向下平移（ ）cm时与⊙O相切．
A．1
B．2
C．3
D．4
【答案】分析：连接OA，由垂径定理和勾股定理得OH=3，当点H平移到点C时，直线与圆相切，求得CH=OC-OH=2cm．
解答：
解：连接OA，
∵OH⊥AB，
∴AH=4，OA=OC=5，
∴OH=3，
∵当点H平移到点C时，直线与圆相切，
∴CH=OC-OH=2cm，
即直线在原有位置向下移动2cm后与圆相切．
故选B．
点评：本题利用了垂径定理，勾股定理，及切线的概念求解．
解答：
解：连接OA，∵OH⊥AB，
∴AH=4，OA=OC=5，
∴OH=3，
∵当点H平移到点C时，直线与圆相切，
∴CH=OC-OH=2cm，
即直线在原有位置向下移动2cm后与圆相切．
故选B．
点评：本题利用了垂径定理，勾股定理，及切线的概念求解．
练习册系列答案
相关题目
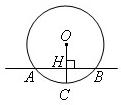8、如图，⊙O的半径OC=5cm，直线l⊥OC，垂足为H，且l交⊙O于A、B两点，AB=8cm，则l沿OC所在直线向下平移与⊙O相切时，移动的距离应等于（ ）
7、如图，⊙O的半径OC=5cm，直线l⊥OC，垂足为H，且l交⊙O于A、B两点，AB=8cm，若l要与⊙O相切，则要沿OC所在直线向下平移（ ）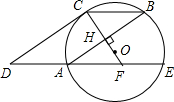
EA延长线于点D，延长CO交AE于点F．
如图，⊙O的半径OC=10cm，直线l⊥CO，垂足为H，交⊙O于A、B两点，AB=16cm，则直线l平移
如图，⊙O的半径OC与直径AB垂直，点P在OB上，CP的延长线交⊙O于点D，在OB的延长线上取点E，使ED=EP．