题目内容
已知在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线交BC边于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°,EC=2BE,判断DE和DC的位置关系,并证明之.

(1)证明:∵AD∥BE,
∴∠1=∠2
 ∵∠1=∠3
∵∠1=∠3
∴∠2=∠3
∴AB=BE
∵AD∥BC,AD=AB
∴AD=BE
∴四边形ABED是平行四边形
∵AB=BE
∴四边形ABED是菱形
(2)DE⊥DC
证明:过点D作DF⊥BC于F,
∵四边形ABED是菱形
∴AB∥DE
∵∠ABC=60°, ∴∠DEC=60°
∴∠EDF=30°
设EF=![]() ,则
,则![]() ,
,![]()
∵DE=2BE=2DE=![]()
∴![]()
在△DFC中,![]()
在△DEC中,![]()
![]()
∴![]() ∴△DEC是直角三角形,∠EDC=90°
∴△DEC是直角三角形,∠EDC=90°
∴DE⊥DC

练习册系列答案
相关题目
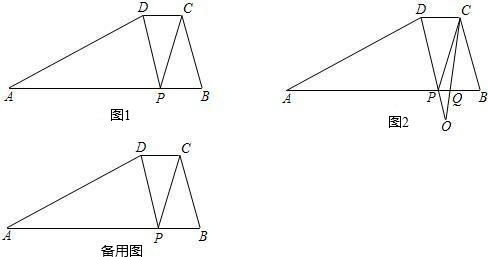
 9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G. ;
;