题目内容
如图,矩形OABC的顶点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了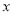 秒.
秒.
(1)当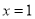 时,求PC的长;
时,求PC的长;
(2)当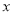 为何值时,△NPC是以PC为腰的等腰三角形?
为何值时,△NPC是以PC为腰的等腰三角形?
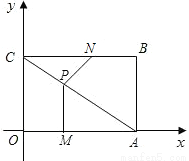
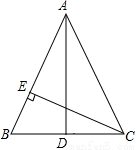
如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.
(1)求证:△ABD∽△CBE;
(2)若BD=3,BE=2,求AC的值.
水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
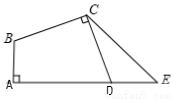
(1)若将这种水果每斤的售价降低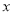 元,则每天的销售量是__________斤(用含
元,则每天的销售量是__________斤(用含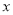 的代数式表示);
的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC.
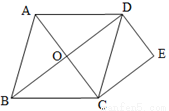
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.
如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
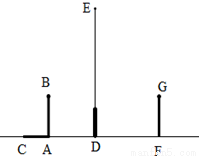
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案 试题属性- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某商品进价a元,商店将价格提高30%作零售价销售,在销售旺季过后,商店以8折的价格开展促销活动,这时一件商品的售价为( )
A. a元 B. 1.04a元 C. 0.8a元 D. 0.92a元
B 【解析】根据题意商品的售价是:a(1+30%)×80%=1.04a元, 故选B.已知|x|=3,|y|=2,且x•y<0,则x+y的值等于( )
A. 5或﹣5 B. 1或﹣1 C. 5或1 D. ﹣5或﹣1
查看答案一个多项式加上多项式2x﹣1后得3x﹣2,则这个多项式为( )
A. x﹣1 B. x+1 C. x﹣3 D. x+3
查看答案下列式子中,不能成立的是( )
A. ﹣(﹣2)=2 B. ﹣|﹣2|=﹣2 C. 23=6 D. (﹣2)2=4
查看答案若有理数a的值在﹣1与0之间,则a的值可以是( )
A. ﹣2 B. 1 C. 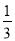 D.
D. 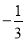
下列运算正确的是( )
A. 3a+2b=5ab B. 3a2b﹣3ba2=0 C. 3x2+2x3=5x5 D. 5y2﹣4y2=1
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列方程是关于x的一元二次方程的是( )
A. ax2+bx+c=0 B. 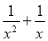 =2 C. x2+2x=x2﹣1 D. 3(x+1)2=2(x+1)
=2 C. x2+2x=x2﹣1 D. 3(x+1)2=2(x+1)
阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
【解析】
∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)已知x2﹣2xy+2y2+6y+9=0,求xy的值;
(2)已知△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣10a﹣12b+61=0,求△ABC的最大边c的值;
(3)已知a﹣b=8,ab+c2﹣16c+80=0,求a+b+c的值.
查看答案某商家预测一种衬衫能畅销市场,就用12000元购进了一批这种衬衫,上市后果然供不应求,商家又用了26400元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但每件进价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫都按每件150元的价格销售,则两批衬衫全部售完后的利润是多少元?
查看答案若x=2m+1,y=3+4m.
(1)请用含x的代数式表示y;
(2)如果x=4,求此时y的值.
查看答案解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.
(1)设A=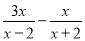 ,B=
,B=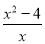 ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案按要求完成下列各题:
(1)已知实数a、b满足(a+b)2=1,(a﹣b)2=9,求a2+b2﹣ab的值;
(2)已知(2015﹣a)(2016﹣a)=2047,试求(a﹣2015)2+(2016﹣a)2的值.
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若x2+mxy+16y2是完全平方式,则m= ________
【解析】试题解析:∵x2+mxy+16y2是完全平方式, ∴m=±8.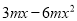 中公因式是___________
中公因式是___________
6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
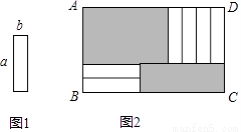
A. a=2b B. a=3b C. a=4b D. a=b
查看答案计算(x2-3x+n)(x2+mx+8)的结果中不含x2和x3的项,则m,n的值为( )
A. m=3,n=1 B. m=0,n=0 C. m=-3,n=-9 D. m=-3,n=8
查看答案若关于x的分式方程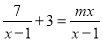 无解,则实数m的值是( )
无解,则实数m的值是( )
A. x=0或1 B. x=1或3 C. x=3或7 D. x=0或3
查看答案某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )
A. 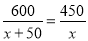 B.
B. 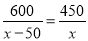 C.
C. 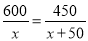 D.
D. 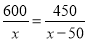
- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若把分式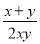 中的x和y都扩大3倍,那么分式的值( )
中的x和y都扩大3倍,那么分式的值( )
A. 扩大3倍 B. 不变 C. 缩小3倍 D. 缩小6倍
C 【解析】试题解析:将3x、3y代入原式,则原式=,所以缩小到原来的, 故选C.与分式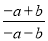 相等的是( )
相等的是( )
A. 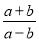 B.
B. 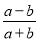 C.
C. 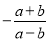 D.
D. 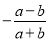
任意给定一个非零数,按下列程序计算,最后输出的结果是( )
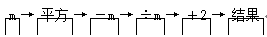
A. m B. m-2 C. m+1 D. m2+1
查看答案下列运算正确的是( )
A. m2(mn-3n+1)=m3n-3m2n B. (-3ab2)2=-9a2b4
C. (-a+b)(-a-b)=b2-a2 D. 3x2y÷xy=3x
查看答案计算(ab2)3的结果,正确的是( )
A. a3b6 B. a3b5 C. ab6 D. ab5
查看答案如图,矩形OABC的顶点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了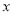 秒.
秒.
(1)当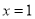 时,求PC的长;
时,求PC的长;
(2)当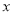 为何值时,△NPC是以PC为腰的等腰三角形?
为何值时,△NPC是以PC为腰的等腰三角形?

- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
(1)画图见解析;(2)DE=4. 【解析】试题分析:(1)连接CB延长CB交DE于O,点O即为所求. (2)连接OG,延长OG交DF于H.线段FH即为所求. (3)根据,可得 ,即可推出DE=4m. 试题解析:(1)【解析】 如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子. (2)【解析】 由已知可得, ,∴,∴OD=4m,∴灯泡的高为4m. ...在一次朋友聚餐中,有A、B、C、D四种素菜可供选择,小明从中选择一种,小莉也从中选择一种(与小明选择的不相同),请利用列表或树状图的方法求出A与B两种素菜被选中的概率.
查看答案直线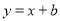 与反比例函数
与反比例函数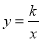 (
(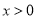 )的图象交于点A(1,2),求这两个函数的表达式.
)的图象交于点A(1,2),求这两个函数的表达式.
解一元二次方程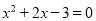
如图,在三角形ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=__________.

函数 是
是 关于
关于 的反比例函数,则
的反比例函数,则 _______.
_______.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
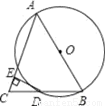
如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.
商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案已知抛物线经过三点A(2,6)、B(-1,0)、C(3,0).
求这条抛物线所对应的二次函数的解析式;
(2)写出它的对称轴和顶点坐标.
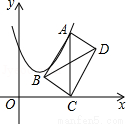
查看答案如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为____.
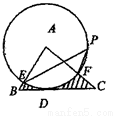
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是__________(结果保留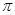 )
)
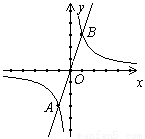
如图,反比例函数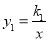 和正比例函数y2=k2x 的图象交于A(-1,-3)、B(1,3)两点,若
和正比例函数y2=k2x 的图象交于A(-1,-3)、B(1,3)两点,若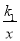 >k2x,则x的取值范围是___________________.
>k2x,则x的取值范围是___________________.
- 题型:解答题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
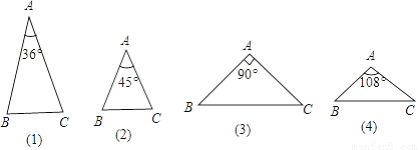
A. (1)(2)(3) B. (1)(3)(4) C. (2)(3)(4) D. (1)(2)(4)
B 【解析】①中作∠B的角平分线即可; ③过A点作BC的垂线即可; ④中以A为顶点AB为一边在三角形内部作一个72度的角即可; 只有②选项不能被一条直线分成两个小等腰三角形. 故选B.如图,PB⊥AB于B,PC⊥AC于C,且PB=PC,则△APB≌△APC的理由是( )
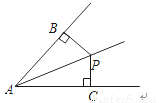
A. SAS B. ASA C. HL D. AAS
查看答案如图,在△ABC中,AB=AC=5,P是BC边上除B,C点外的任意一点,则代数式AP2+PB·PC等于 ( )
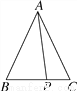
A. 25 B. 15 C. 20 D. 30
查看答案如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
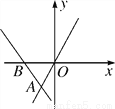
A. x<-2 B. -2<x<-1 C. -2<x<0 D. -1<x<0
查看答案若直线y=3x+6与直线y=2x+4的交点坐标为(a , b),则解为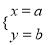 的方程组是( )
的方程组是( )
A. 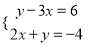 B.
B. 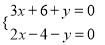 C.
C. 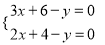 D.
D. 
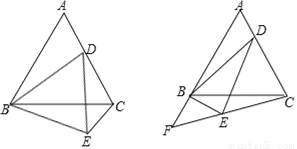
如图,已知等边△ABC中,D为边AC上一点.
(1)以BD为边作等边△BDE,连接CE,求证:AD=CE;
(2)如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF;
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

