题目内容
如图，直线MN切⊙O于A，AB是⊙O的弦，∠MAB的平分线交⊙O于C，连接CB并延长交MN于N，如果AN=6，NB=4，那么弦AB的长是（ ）
A．
B．3
C．5
D．
【答案】分析：直线MN切⊙O于A，根据切割线定理得到AN2=BN•NC，因而可求得NC=9，BC=5，根据∠MAB的平分线交⊙O于C，则根据弦切角定理，据∠NAB=∠C，可证明△ABN∽△CAN，利用相似的性质可知
，列方程即可求解．
解答：解：∵AN2=BN•NC，NC=9
∴BC=5
∵∠MAC=∠B
∴∠BAC=∠ABC
∵AC=BC=5，∠NAB=∠C
∴△ABN∽△CAN
∴
∴
解得AB=
．
故选D．
点评：本题主要考查了弦切角定理，从而转化为三角形相似的问题．
，列方程即可求解．解答：解：∵AN2=BN•NC，NC=9
∴BC=5
∵∠MAC=∠B
∴∠BAC=∠ABC
∵AC=BC=5，∠NAB=∠C
∴△ABN∽△CAN
∴
∴
解得AB=
．故选D．
点评：本题主要考查了弦切角定理，从而转化为三角形相似的问题．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
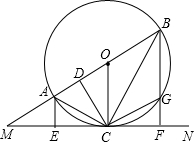，BF⊥MN，E、F分别为垂足，BF交⊙O于G，连接AC、BC，过点C作CD⊥AB，D为垂足，连接OC、CG．下列结论，其中正确的有（ ）
如图，直线MN切⊙O于A，AB是⊙O的弦，∠MAB的平分线交⊙O于C，连接CB并延长交MN于N，如果AN=6，NB=4，那么弦AB的长是（ ）
