题目内容
如图,三角板ABC的两直角边AC,BC的长分别是40cm和30cm,点G在斜边AB上,且BG=30cm,将这个三角板以G为中心按逆时针旋转90°,至△A′B′C′的位置,那么旋转后两个三角板重叠部分(四边形EFGD)的面积为 cm2.
【答案】
144
【解析】
试题分析:由勾股定理得AB= =
= =50,
=50,
又∵BG=30,
∴AG=AB﹣BG=20,
由△ADG∽△ABC得, =
= =
= ,即
,即 =
= =
= ,
,
解得DG=15,AD=25,
A′D=A′G﹣DG=AG﹣GD=20﹣15=5,
由△A′DE∽△A′B′C′,可知 =
= =
= ,
,
由△A′GF∽△A′C′B′,可知
根据相似三角形面积比等于相似比的平方,可知
S四边形EFGD=S△A′FG﹣S△A′DE= S△A′B′C′﹣
S△A′B′C′﹣ S△A′B′C′=
S△A′B′C′= ×
× ×40×30=144cm2.
×40×30=144cm2.
考点:旋转的性质;勾股定理;相似三角形的判定与性质.
点评:本题考查了旋转图形的面积不变,勾股定理、相似三角形的性质的运用.

练习册系列答案
相关题目
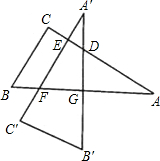 如图,三角板ABC的两直角边AC,BC的长分别是40cm和30cm,点G在斜边AB上,且BG=30cm,将这个三角板以G为中心按逆时针旋转90°,至△A′B′C′的位置,那么旋转后两个三角板重叠部分(四边形EFGD)的面积为
如图,三角板ABC的两直角边AC,BC的长分别是40cm和30cm,点G在斜边AB上,且BG=30cm,将这个三角板以G为中心按逆时针旋转90°,至△A′B′C′的位置,那么旋转后两个三角板重叠部分(四边形EFGD)的面积为

