Question

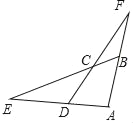
【题目】如图，已知四边形ABCD的一组对边AD、BC的延长线相交于点E．另一组对边AB、DC的延长线相交于点F，若cos∠ABC=cos∠ADC=，CD=5，CF=ED=n，则AD的长为_____（用含n的式子表示）．

Answer 1

【答案】

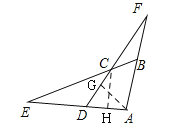
【解析】分析：作辅助线，构建直角三角形，利用三角函数计算DH和CH的长，并设AD=5a，则DG=3a，AG=4a，证明△AFG∽△CEH，列比例式可得a的值，从而得AD的长．

详解：过C作CH⊥AD于H．

∵cos∠ADC=，CD=5，∴DH=3，∴CH=4，∴tan∠E==，

过A作AG⊥CD于G，设AD=5a，则DG=3a，AG=4a，

∴FG=DF﹣DG=5+n﹣3a．

∵CH⊥AD，AG⊥DF．

∵∠CHE=∠AGF=90°．

∵∠ADC=∠ABC，∴∠EDC=∠CBF．

∵∠DCE=∠BCF，∴∠E=∠F，∴△AFG∽△CEH，

∴，∴a=，∴AD=5a=．

故答案为：．