Question

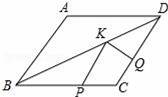
如图，矩形纸片ABCD，AB=3，AD=5，折叠纸片，使点A落在BC边上的E处，折痕为PQ，当点E在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点E在BC边上可移动的最大距离为（　　）

A．1    B．2    C．4    D．5

Answer 1

B

【考点】翻折变换（折叠问题）．

【分析】根据翻折变换，当点Q与点D重合时，点A′到达最左边，当点P与点B重合时，点A′到达最右边，所以点A′就在这两个点之间移动，分别求出这两个位置时A′B的长度，然后两数相减就是最大距离．

【解答】解：如图1，当点D与点Q重合时，根据翻折对称性可得

ED=AD=5，

在Rt△ECD中，ED²=EC²+CD²，

即5²=（5﹣EB）²+3²，

解得EB=1，

如图2，当点P与点B重合时，根据翻折对称性可得EB=AB=3，

∵3﹣1=2，

∴点E在BC边上可移动的最大距离为2．

故选B．