题目内容
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧 上有一点E使∠EBC=∠DEC,延长BE依次交AC于G,交⊙O于H.
上有一点E使∠EBC=∠DEC,延长BE依次交AC于G,交⊙O于H.
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CG和CE的长.
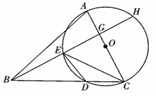

证明:⑴连接AD
∵∠DAC=∠DEC ∠EBC=∠DEC ∴∠DAC=∠EBC
又∵AC是⊙O的直径 ∴∠ADC=90° ∴∠DCA+∠DAC=90°
∴∠EBC+∠DCA=90° ∴∠BGC=180°-(∠EBC+∠DCA)=180°-90°=90°
∴AC⊥BH
⑵∵∠BDA=180°-∠ADC=90°∠ABC=45°
∴∠BAD=45° ∴BD=AD
∵BD=8 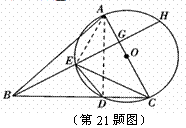

∴AD=8
又∵∠ADC=90° AC=10 ∴由勾股定理,得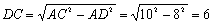 .
.
∴BC=BD+DC=8+6=14
又∵∠BGC=∠ADC=90° ∠BCG=∠ACD
∴△BCG∽△ACD ∴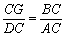 ∴
∴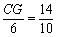 ∴
∴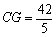
连结AE,∵AC是直径 ∴∠AEC=90°
又∵EG⊥AC
∴△CEG∽△CAE ∴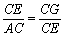 ∴
∴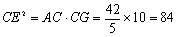
∴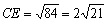 .
.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案若 ,则
,则 的值为( )
的值为( )
| A. |
| B. |
| C. |
| D. |
|
 C.
C. D.
D. .
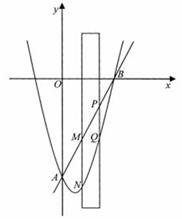
.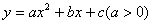 经过点M(-1,2)和点N(1,-2),交x轴于
经过点M(-1,2)和点N(1,-2),交x轴于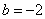 ;
; 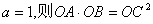

 的所有正整数解________________.
的所有正整数解________________.



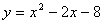 交
交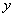 轴于点A,交
轴于点A,交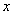 轴正半轴于点B.
轴正半轴于点B. ;且
;且 .试比较线段MN与PQ的大小.
.试比较线段MN与PQ的大小.