题目内容

已知在平面直角坐标系中，直线               与x轴，y轴相交于A,B两点，
直线       与AB相交于C点，点D从点O出发，以每秒1个单位的速度沿x轴向右运
动到点A，过点D作x轴的垂线，分别交直线        和直线               于P,Q两点（P点不与C点重合），以PQ为边向左作正△PQR，设正△PQR与△OBC重叠部分的面积为S（平方单位），点D的运动时间为t（秒）
（1）求点A,B,C的坐标； （2）若点           正好在△PQR的某边上，求t的值；
（3）求S关于t的函数关系式，并写出相应t的取值范围，     
求出D在整个运动过程中s的最大值。

① A（6,0）   B （0，）                    

② ， ，  
③
因为S的最大值在范围内取到，，开口向下，对称轴直线x=9，函数的自变量部分图像在对称轴的左侧，S随t的增大而增大
∴当t=6时，。

解析

练习册系列答案
相关题目
已知在平面直角坐标系中，点A，点B的坐标分别为A（0，0），B（0，4），点C在x轴上，且△ABC的面积为6，求点C的坐标．
已知在平面直角坐标系xOy中，二次函数y=x2-bx+c（b＞0）的图象经过点A（-1，b），与y轴相交于点B，且∠ABO的余切值为3．
（1）求点B的坐标；
（2）求这个函数的解析式；
（3）如果这个函数图象的顶点为C，求证：∠ACB=∠ABO．
精英家教网已知在平面直角坐标系xOy中，⊙O的半径为1．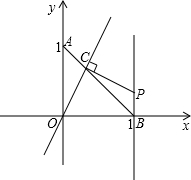
（1）当直线l：y=x+b与⊙O只有一个交点时，求b的值；
（2）当反比例函数y=
kx
的图象与⊙O有四个交点时，求k的取值范围；
（3）试探究当n取不同的数值时，二次函数y=x2+n的图象与⊙O交点个数情况．
如图，已知在平面直角坐标系中，点A的坐标为（0，1），点B的坐标为（1，0），经过原点的精英家教网直线交线段AB于点C，过点C作OC的垂线与直线x=1相交于点P，设AC=t，点P的坐标为（1，y），
（1）求点C的坐标（用含t的代数式表示）；
（2）求y与t之间的函数关系式和t的取值范围；
（3）当△PBC为等腰三角形时，直接写出点P的坐标．
如图，已知在平面直角坐标系中，平行四边形ABCD顶点A（0，0），C（10，4），直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网