题目内容
15.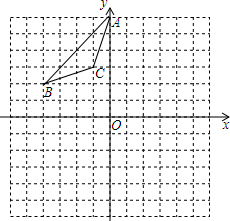 如图,△ABC的三个顶点的坐标分别为A(0,6),B(-4,2),C(-1,3).
如图,△ABC的三个顶点的坐标分别为A(0,6),B(-4,2),C(-1,3).(1)画出与△ABC关于y轴对称的△AB1C1,并写出点B1的坐标;
(2)在x轴上找出点P,使PC+PB1最小,并直接写出点P的坐标.(保留必要作图痕迹)
分析 (1)作出各点关于y轴的对称点,再顺次连接即可;
(2)作点C关于x轴的对称点C′,连接B1C′交x轴于点P,则点P即为所求点.
解答 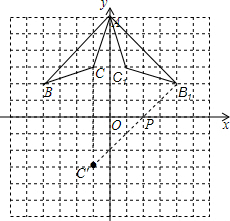 解:(1)如图,△AB1C1即为所求;
解:(1)如图,△AB1C1即为所求;
(2)∵C(-1,3),
∴C′(-1,-3).
设直线B1C′的解析式为y=kx+b(k≠0),
∵B1(4,2),
∴$\left\{\begin{array}{l}-3=-k+b\\ 2=4k+b\end{array}\right.$,解得$\left\{\begin{array}{l}k=1\\ b=-2\end{array}\right.$,
∴直线B1C′的解析式为y=x-2,
∴当y=0时,x=2,
∴P(2,0).
点评 本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
5.如图图案都是同样大小的小正方形按一定的规律组成的,其中第1个图形中有5个小正方形,第2个图形有13个小正方形,第3个图形有25个小正方形,…,按此规律,则第8个图形中小正方形的个数为( )
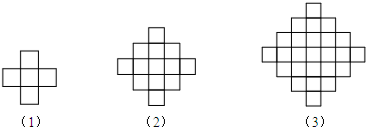
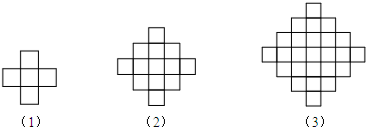
| A. | 181 | B. | 145 | C. | 100 | D. | 88 |
6. 如图,图中的长方形共有( )个.
如图,图中的长方形共有( )个.
 如图,图中的长方形共有( )个.
如图,图中的长方形共有( )个.| A. | 9 | B. | 8 | C. | 5 | D. | 4 |