题目内容
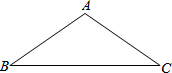已知△ABC中，AB=AC=6cm，BC=8cm，以点A为圆心，以4cm长为半径作圆，则⊙A与BC的位置关系是（ ）| A、相离 | B、相切 | C、相交 | D、外离 |
考点：直线与圆的位置关系
专题：
分析：此题只需根据等腰三角形的三线合一和勾股定理，求得圆心到直线的距离，再根据数量关系进行判断．
若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．
若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．
解答：
解：作AD⊥BC于D．
根据等腰三角形的三线合一，得BD=4cm；
再根据勾股定理得AD=2
cm，
∵2
＞4cm
∴以4cm为半径的⊙A与BC所在直线的位置关系是相离．
故选D．
解：作AD⊥BC于D．根据等腰三角形的三线合一，得BD=4cm；
再根据勾股定理得AD=2
| 5 |
∵2
| 5 |
∴以4cm为半径的⊙A与BC所在直线的位置关系是相离．
故选D．
点评：考查了直线和圆的位置关系与数量之间的联系．能够综合运用等腰三角形的性质和勾股定理求解．
练习册系列答案
阅读快车系列答案
相关题目
在平面直角坐标系xOy中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒若二次根式
在实数范围内有意义，则x的取值范围为（ ）
| 6-2x |
| A、x≥3 | B、x≤3 |
| C、x≥-3 | D、x≤-3 |
如图在Rt△ABC中，∠ACB=90°，∠A=30°，将△ABC绕点C按顺时针方向旋转一定角度后得到△EDC，此时点D在AB边上，斜边DE交AC边于点F，则旋转的角度为（ ）| A、30° | B、45° |
| C、60° | D、75° |
通过平移，可将图1中的福娃“欢欢”移动到图（ ）A、 |
B、 |
C、 |
D、 |
如图，在平面直角坐标系中，点P的坐标是（ ）| A、（-2，-1） |
| B、（-2，1） |
| C、（-1，2） |
| D、（1，-2） |
线段CD是由线段AB平移得到的，点A（1，2）的对应点C（3，4），则点B（4，7）的对应点D的坐标为（ ）
| A、（-1，0） |
| B、（6，9） |
| C、（0，-1） |
| D、（9，6） |
如图，在数轴上表示-1，-| 2 |
A、1-
| ||
B、2-
| ||
C、
| ||
D、
|