题目内容
如图,直线l1过点A(0,4),点D(4,0),直线l2: 与x轴交于点C,两直线l1,l2相交于点B。
与x轴交于点C,两直线l1,l2相交于点B。
(1)求直线l1的解析式和点B的坐标;
(2)求△ABC的面积。
 与x轴交于点C,两直线l1,l2相交于点B。
与x轴交于点C,两直线l1,l2相交于点B。(1)求直线l1的解析式和点B的坐标;
(2)求△ABC的面积。

解:(1)设l1的解析式为:ax+b=y
∵l1经过A(0,4),D(4,0)
∴将A、B代入解析式得:b=44a+b=0
∴a=-1,b=4
即l1的解析式为:y=-x+4;
(2)l1与l2联立 得B(2,2)
得B(2,2)
C是l2与x轴的交点,在y= x+1中所以令y=0,得C(-2,0)
x+1中所以令y=0,得C(-2,0)
∴|CD|=6,|AO|=4,B到X的距离为2
∵AO⊥CD
∴△ACD的面积为 |AO||CD|=
|AO||CD|= ×4×6=12 ①
×4×6=12 ①
△CBD的面积为 ×B到X轴的距离×CD=
×B到X轴的距离×CD= ×2×6=6 ②
×2×6=6 ②
∴△ABC的面积为①-②=6。
∵l1经过A(0,4),D(4,0)
∴将A、B代入解析式得:b=44a+b=0
∴a=-1,b=4
即l1的解析式为:y=-x+4;
(2)l1与l2联立
 得B(2,2)
得B(2,2)C是l2与x轴的交点,在y=
 x+1中所以令y=0,得C(-2,0)
x+1中所以令y=0,得C(-2,0)∴|CD|=6,|AO|=4,B到X的距离为2
∵AO⊥CD
∴△ACD的面积为
 |AO||CD|=
|AO||CD|= ×4×6=12 ①
×4×6=12 ①△CBD的面积为
 ×B到X轴的距离×CD=
×B到X轴的距离×CD= ×2×6=6 ②
×2×6=6 ②∴△ABC的面积为①-②=6。

练习册系列答案
相关题目
 点C,两直线l1,l2相交于点B.
点C,两直线l1,l2相交于点B. 如图,直线l1过点A(0,4),点D(4,0),直线l2:
如图,直线l1过点A(0,4),点D(4,0),直线l2: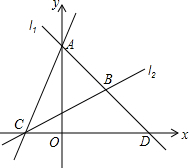 如图,直线l1过点A(0,4)、D(4,0)两点,直线l2:y=
如图,直线l1过点A(0,4)、D(4,0)两点,直线l2:y=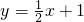 与x轴交于
与x轴交于 点C,两直线l1,l2相交于点B.
点C,两直线l1,l2相交于点B.