Question

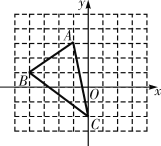
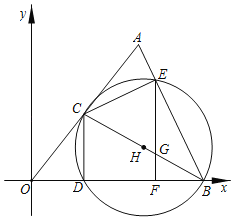
【题目】如图，在平面直角坐标系中，A（3，4），B（5，0），连结AO，AB．点C是线段AO上的动点（不与A，O重合），连结BC，以BC为直径作⊙H，交x轴于点D，交AB于点E，连结CD，CE，过E作EF⊥x轴于F，交BC于G．

（1）AO的长为　 　，AB的长为　 　（直接写出答案）

（2）求证：△ACE∽△BEF；

（3）若圆心H落在EF上，求BC的长；

（4）若△CEG是以CG为腰的等腰三角形，求点C的坐标．

Answer 1

【答案】（1）5，2；（2）见解析；（3）4；（4）（，），（，）

【解析】

（1）利用两点间距离公式计算即可；

（2）根据两角对应相等的两个三角形相似即可判断；

（3）当GC＝GE时，点G与点H重合，根据三角函数和勾股定理解答即可；

（4）分两种情形画出图形,利用锐角三角函数和相似三角形的性质分别求解即可解决问题．

解：（1）∵A（3，4），B（5，0）．

∴OA＝＝5，OB＝5，AB＝．

故答案为：5；2．

（2）如图1中，

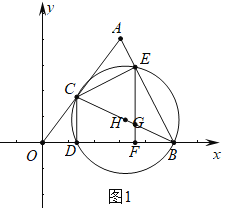
∵OA＝OB＝5，

∴∠A＝∠EBF，

∵BC是直径，

∴∠BEC＝∠AEC＝90°，

∵EF⊥OB，

∴∠EFB＝90°，

∴∠AEC＝∠EFB＝90°，

∴△ACE∽△BEF；

（3）如图2中，当GC＝GE时，点G与点H重合，

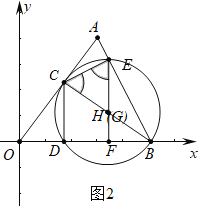
∴GE＝GB＝GC，

∴∠GEB＝∠EBG，

∵∠GEB+∠ABO＝90°，

∴∠EBG+∠ABO＝90°，

∵OA＝OB，

∴∠A＝∠OBA，

∴∠A+∠EBG＝90°，

∴∠ACB＝90°，

∴BC⊥AO，

∴OC＝OBcos∠AOB，

∵A（3，4），OA=5，

∴cos∠AOB＝，

∴OC＝5×=3，

∴BC＝=；

（4）①如图2中，当GC＝GE时，点G与点H重合，

∴GE＝GB＝GC，

∴∠GEB＝∠EBG，

∵∠GEB+∠ABO＝90°，

∴∠EBG+∠ABO＝90°，

∵OA＝OB，

∴∠A＝∠OBA，

∴∠A+∠EBG＝90°，

∴∠ACB＝90°，

∴BC⊥AO，

∵A（3，4），OA=5，

∴cos∠AOB＝，

∴OC＝OBcos∠AOB=5×＝3，

∴OD= OCcos∠AOB=3×＝，CD==，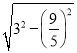

∴C（，）．

②如图3中，当CE＝CG时，作AK⊥OB于K．设CD＝4k，OD＝3k．

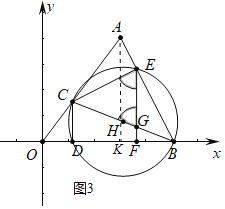
∵A（3，4），B（5，0），

∴AK=4，OK=3，OB=5，BK=2，

∵CE＝CG，

∴∠CEG＝∠CGE＝∠BGF，

∵∠CEG+∠BEF＝90°，∠BGF+∠CBD＝90°，

∴∠CBD＝∠BEF，

∵EF⊥OB，AK⊥OB，

∴EF∥AK，

∴∠BEF＝∠BAK，

∴∠CBD＝∠BAK，

∵∠CDB＝∠AKB＝90°，

∴△CBD∽△BAK，

∴，

∴，

∴k＝，

∴C（，）．