题目内容
在如图所示的直角坐标系中,O为原点,直线y=-| 1 |
| 2 |
 且点B的坐标为(0,8).
且点B的坐标为(0,8).(1)求m的值;
(2)设直线OP与线段AB相交于P点,且
| S△AOP |
| S△BOP |
| 1 |
| 3 |
分析:(1)根据B点的坐标即可求出m的值.
(2)根据△AOP和△BOP的面积之比求出AP与BP的比值,再过点P做PC⊥OA垂足为点C,求出OC的长即可求出点P的坐标.
(2)根据△AOP和△BOP的面积之比求出AP与BP的比值,再过点P做PC⊥OA垂足为点C,求出OC的长即可求出点P的坐标.
解答: 解:(1)∵直线y=-
解:(1)∵直线y=-
x+m与y轴交于B点,点B的坐标为(0,8).
∴m=8
(2)∵
=
,
∴
=
过点P做PC⊥OA垂足为点C,
则
=
=
∵直线y=-
x+8与x轴交于A点,
∴点A的坐标为(16,0).
∴OA=16
∴OC=16×
=12
∴点P的横坐标为12
∵点P在直线y=-
x+8上
∴点P的纵坐标为y=-
×12+8=2
∴点P的坐标为(12,2).
 解:(1)∵直线y=-
解:(1)∵直线y=-| 1 |
| 2 |
∴m=8
(2)∵
| S△AOP |
| S△BOP |
| 1 |
| 3 |
∴
| AP |
| BP |
| 1 |
| 3 |
过点P做PC⊥OA垂足为点C,
则
| AC |
| OC |
| AP |
| BP |
| 1 |
| 3 |
∵直线y=-
| 1 |
| 2 |
∴点A的坐标为(16,0).
∴OA=16
∴OC=16×
| 3 |
| 4 |
∴点P的横坐标为12
∵点P在直线y=-
| 1 |
| 2 |
∴点P的纵坐标为y=-
| 1 |
| 2 |
∴点P的坐标为(12,2).
点评:本题主要考查了一次函数的图象和性质,解题时要注意有关知识的综合应用.

练习册系列答案
相关题目
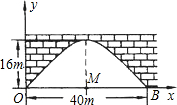 如图,有一个抛物线的拱形立交桥,这个桥拱的最大高度为16m,跨度为40m,现把它放在如图所示的直角坐标系里,若要在离跨度中心点M5m处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长?
如图,有一个抛物线的拱形立交桥,这个桥拱的最大高度为16m,跨度为40m,现把它放在如图所示的直角坐标系里,若要在离跨度中心点M5m处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长?