题目内容
在?ABCD中，AD=2DC，M、N分别在BA、AB的延长线上，且MA=AB=BN，则MC与DN的关系是
- A.相等
- B.垂直
- C.垂直且相等
- D.不能确定
B
分析：假设MC和AD交于E，DN和BC交于F，由题可知△AME≌△DCE，即AE=DE=
AD，同理BF=CF=BC，所以EF=MA=ED，且和AB平行，即四边形EFCD为菱形，因此对角线EC⊥FD，即MC和DN垂直．至于它们的数量关系，随着图形的变化，也随之变化，无法确定．
解答：
解：设MC与AD交于E点，ND与BC交于F点，连接EF，
∵MA=AB，AB=CD，
∴MA=CD，又MA∥CD，
∴△AME≌△DCE，
∴AE=ED=AD=DC，
同理可证，FC=DC；
∴FC=ED，又FC∥ED，
∴四边形EFCD是平行四边形，又FC=DC，
∴?EFCD是菱形；
根据菱形“对角线互相垂直”的性质可知，MC⊥DN．
故选B．
点评：此题考查了平行四边形以及菱形的判定和性质，利用菱形对角线互相垂直这一性质，可以证明线与线的垂直关系．
分析：假设MC和AD交于E，DN和BC交于F，由题可知△AME≌△DCE，即AE=DE=
AD，同理BF=CF=BC，所以EF=MA=ED，且和AB平行，即四边形EFCD为菱形，因此对角线EC⊥FD，即MC和DN垂直．至于它们的数量关系，随着图形的变化，也随之变化，无法确定．解答：
解：设MC与AD交于E点，ND与BC交于F点，连接EF，∵MA=AB，AB=CD，
∴MA=CD，又MA∥CD，
∴△AME≌△DCE，
∴AE=ED=
AD=DC，同理可证，FC=DC；
∴FC=ED，又FC∥ED，
∴四边形EFCD是平行四边形，又FC=DC，
∴?EFCD是菱形；
根据菱形“对角线互相垂直”的性质可知，MC⊥DN．
故选B．
点评：此题考查了平行四边形以及菱形的判定和性质，利用菱形对角线互相垂直这一性质，可以证明线与线的垂直关系．
练习册系列答案
相关题目
15、如图，在?ABCD中，AD=7，AB=4，AE平分∠BAD交BC边于点E，则线段BE，EC的长度分别为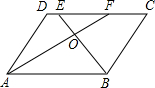
如图，在?ABCD中，AD=4，AB=6，AF是∠BAD的平分线，交DC于F，BE是∠ABC的平分线，交DC于E，AF与BE相交于点O，则S△EOF：S△AOB等于（ ）
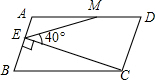如图所示，在?ABCD中，AD=2AB，M是AD的中点，CE⊥AB于E，∠CEM=40°，则∠DME是
