题目内容
如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作EF∥BC，交AB、AC于E、F，若EF=8，BE=3，则CF=5
5
．分析：根据平行线的性质和角平分线的性质，解出△BED和△CFD是等腰三角形，通过等量代换即可得出结论．
解答：
解：∵△ABC中BD、CD平分∠ABC、∠ACB，
∴∠1=∠2，∠5=∠6，
∵EF∥BC，∴∠2=∠3，∠4=∠6，
∴∠1=∠3，∠4=∠5，
根据在同一三角形中等角对等边的原则可知，BE=ED，DF=FC，故EF=ED+DF=BE+CF．
∵EF=8，BE=3，
∴CF=EF-BE=8-3=5，
故答案为5．
解：∵△ABC中BD、CD平分∠ABC、∠ACB，∴∠1=∠2，∠5=∠6，
∵EF∥BC，∴∠2=∠3，∠4=∠6，
∴∠1=∠3，∠4=∠5，
根据在同一三角形中等角对等边的原则可知，BE=ED，DF=FC，故EF=ED+DF=BE+CF．
∵EF=8，BE=3，
∴CF=EF-BE=8-3=5，
故答案为5．
点评：本题综合考查等腰三角形的性质及平行线的性质；一般是利用等腰（等边）三角形的性质得出相等的边，进而得出结论．进行等量代换是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，当∠A的位置及大小变化时，线段EF和BE+CF的大小关系（ ）| A、EF＞BE+CF | B、EF=BE+CF | C、EF＜BE+CF | D、不能确定 |
8、如图，△ABC中BD是角平分线，∠A=∠CBD=36°，则图中等腰三角形有（ ）
19、如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，求证：EF=BE+CF．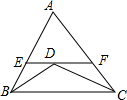
如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，AB=5，AC=7，BC=8，△AEF的周长为（ ）