题目内容
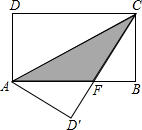
如图,一货轮在海上由西往东行驶,从A、B两个小岛中间穿过.当货轮行驶到点P处时,测得小岛A在正北方向,小岛B位于南偏东24.5°方向;货轮继续前行12海里,到达点Q处,又测得小岛A位于北偏西49°方向,小岛B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°≈0.75)

(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°≈0.75)

(1)相等,理由见解析;(2)20海里.
试题分析:(1)分别求出∠QPB和∠QBP的度数,可得∠BPQ=∠PBQ,即可得出PQ=BQ;
(2)在Rt△APQ中,根据PQ的长度和∠AQP,利用三角函数求出AQ的长度,然后根据已知角的度数得出∠AQB=90°,在Rt△AQB中,解直角三角形,即可求得AB的长度.
(1)线段BQ与PQ相等.
证明如下:∵∠PQB=90°-41°=49°,
∴∠BPQ=90°-24.5°=65.5°,
∠PBQ=180°-49°-65.5°=65.5°,
∴∠BPQ=∠PBQ,
∴BQ=PQ;
(2)在Rt△APQ中,
∵∠PQA=90°-49°=41°,
∴AQ=
 (海里),
(海里),又∵∠AQB=180°-49°-41°=90°,
∴△ABQ是直角三角形,
∵BQ=PQ=12海里,
∴AB2=AQ2+BQ2=162+122,
∴AB=20(海里),
答:A、B的距离为20海里.

练习册系列答案
相关题目

 (i=1:
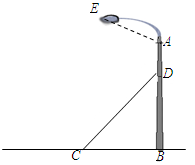
(i=1: 是指坡面的铅直高度BH与水平宽度AH的比),AB=10米,AE=15米.求广告牌CD的高度.
是指坡面的铅直高度BH与水平宽度AH的比),AB=10米,AE=15米.求广告牌CD的高度.
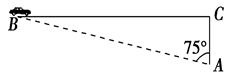
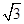 ≈1.732,60千米/小时≈16.7米/秒)
≈1.732,60千米/小时≈16.7米/秒)