题目内容
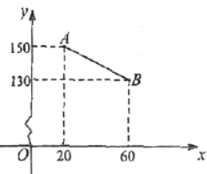
【题目】课外阅读是提高学生素养的重要途径．某校为了了解学生课外阅读情况，随机抽查了
名学生，统计他们平均每天课外阅读时间
．根据
的长短分为
，
，
，
四类，下面是根据所抽查的人数绘制的两幅不完整的统计图表．请根据图表中提供的信息，解答下面的问题：
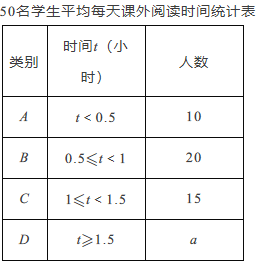
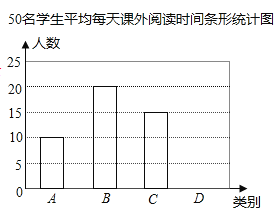
（1）本次调查的样本容量为_______；
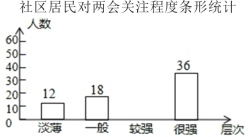
（2）求表格中的
的值，并在图中补全条形统计图（如图）；
（3）该校现有
名学生，请你估计该校共有多少名学生的课外阅读时间不少于
？
【答案】（1）
；（2）5，补全统计图见解析；（3）520名.
【解析】
（1）直接根据题意写出样本容量即可；
（2）用抽查的学生的总人数减去A，B，C三类的人数即为D类的人数也就是a的值，并补全统计图；
（3）先求出课外阅读时间不少于1小时的学生占的比例，再乘以1300即可．
（1）本次调查的样本容量为50；
（2）50-10-20-15=5（名），
故a的值为5，条形统计图如下：
（3）
（名）
答：估计该校共有
名学生的课外阅读时间不少于
．
【题目】某校了解九年级学生近两个月“推荐书目”的阅读情况，随机抽取了该年级的部分学生，调查了他们每人“推荐书目”的阅读本数．设每名学生的阅读本数为n，并按以下规定分为四档：当n＜3时，为“偏少”；当3≤n＜5时，为“一般”；当5≤n＜8时，为“良好”；当n≥8时，为“优秀”．将调查结果统计后绘制成不完整的统计图表：
阅读本数n（本） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数（名） | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题：
（1）分别求出统计表中的x、y的值；
（2）估计该校九年级400名学生中为“优秀”档次的人数；
（3）从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会，请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率．
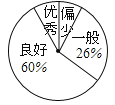
【题目】为了了解学生关注热点新闻的情况，“两会”期间，小明对班级同学一周内收看“两会”新闻的次数情况作了调查，调查结果统计如图所示（其中男生收看
次的人数没有标出）.
根据上述信息，解答下列各题：
×
（1）该班级女生人数是__________，女生收看“两会”新闻次数的中位数是________；
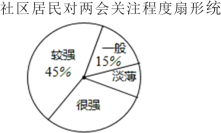
（2）对于某个群体，我们把一周内收看某热点新闻次数不低于次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
，试求该班级男生人数；
（3）为进一步分析该班级男、女生收看“两会”新闻次数的特点，小明给出了男生的部分统计量（如表）.
统计量 | 平均数（次） | 中位数（次） | 众数（次） | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识，适当计算女生的有关统计量，进而比较该班级男、女生收看“两会”新闻次数的波动大小.