Question

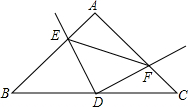
如图，△ABC中，BD、CE是△ABC的两条高，点F、M分别是DE、BC的中点．求证：FM⊥DE．

Answer 1

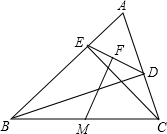
证明：连接MD、ME．
∵BD是△ABC的高，M为BC的中点，
∴在Rt△CBD中，MD=

1

2

BC，（直角三角形斜边上那的中线等于斜边的一半）
同理可得ME=

1

2

BC，
∴MD=ME，
∵F是DE的中点，（等腰三角形三线合一）
∴FM⊥DE．