Question

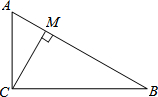
如图，△ABC中，∠A=90°，AB=AC=2，D是BC中点，以D为端点，引两条射线DE、DF分别交AB、AC于E、F点，若DE⊥DF，则EF的最小值为______．

Answer 1

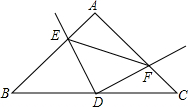
如图，连接AD，∵AB=AC，D是BC中点，
∴AD平分∠BAC，
过点D作DG⊥AB于G，作DH⊥AC于H，
则DG=DH，
又∵∠BAC=90°，
∴∠GDH=90°，
∴∠EDG+∠EFH=90°，
∵DE⊥DF，
∴∠FDH+∠EFH=90°，
∴∠EDG=∠FDH，
在△EDG和△FDH中，

∠EDG=∠FDH ∠EGD=∠FHD=90° DG=DH

，
∴△EDG≌△FDH（AAS），
∴DE=DF，
∴△DEF是等腰直角三角形，
∵D是BC中点，DG⊥AB，∠BAC=90°，
∴DG是△ABC的一条中位线，
∴DG=

1

2

AC=

1

2

×2=1，
根据垂线段最短，当DE和DG重合时EF最小，此时EF=

2

DE=

2

×1=

2

．
故答案为：

2

．