Question

【题目】图象经过三点，和()的函数只可能是(　　)

A.正比例函数B.一次函数C.反比例函数D.二次函数

Answer 1

【答案】D

【解析】

依次分析正比例函数，一次函数，可得出这三点不在同一直线上，故不可能是正比例函数和一次函数，若为反比例函数，分析可得出互相矛盾的结论，故只能是二次函数.

解：设A,B,C（），函数的图象过点A和B，

（1）若为正比例函数，设解析式为y=kx, 函数的图象过点A和B，,易得k=3,

∴y=3x,

把B代入，得,

解得，则，即C（3，-4），

易知C（3，-4）不在直线y=3x上，故这个函数不可能是正比例函数；

（2）若为一次函数，且过点B和点C（）,设y=kx+b,则有：,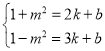

解得：（）

则当x=1时，

所以A不在直线上，

故这个函数不可能是一次函数；

（3）若为反比例函数，设，将A代入可得k=4,即

将B代入，可得，

将C代入，可得，与前面矛盾且无解，

故这个函数不可能是反比例函数；

（4）综上可知，点A,B,C不在同一直线上，因此过这三点可得一抛物线，即这个函数只可能是二次函数.

故选：D