题目内容
 如图,①请你填写一个适当的条件:________,使AD∥BC.②若AD∥BC,△ABD是等腰三角形,当∠ABC=70°时,∠ADB=________°.
如图,①请你填写一个适当的条件:________,使AD∥BC.②若AD∥BC,△ABD是等腰三角形,当∠ABC=70°时,∠ADB=________°.
∠FAD=∠ABC或∠ADB=∠DBC或∠DAB+∠ABC=180° 35
分析:①本题的开放性试题,可根据同位角相等、内错角相等和同旁内角互补来添加条件.
②根据等腰三角形的性质及平行线的性质即可得到答案.
解答:①∵内错角相等,两直线平行,
∴∠ADB=∠DBC(或∠FAD=∠ABC或∠ADB=∠DBC或∠DAB+∠ABC=180°),则AD∥BC.
②∵△ABD是等腰三角形,
∴AB=AD,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴BD平分∠ABC,
∵∠ABC=70°,
∴∠ABD=35°,
故答案为:∠FAD=∠ABC或∠ADB=∠DBC或∠DAB+∠ABC=180°,35°.
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两条被截直线平行.
分析:①本题的开放性试题,可根据同位角相等、内错角相等和同旁内角互补来添加条件.
②根据等腰三角形的性质及平行线的性质即可得到答案.
解答:①∵内错角相等,两直线平行,
∴∠ADB=∠DBC(或∠FAD=∠ABC或∠ADB=∠DBC或∠DAB+∠ABC=180°),则AD∥BC.
②∵△ABD是等腰三角形,
∴AB=AD,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴BD平分∠ABC,
∵∠ABC=70°,
∴∠ABD=35°,
故答案为:∠FAD=∠ABC或∠ADB=∠DBC或∠DAB+∠ABC=180°,35°.
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两条被截直线平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 16、如图,若AD∥BC,请你填写一个适当的条件:
16、如图,若AD∥BC,请你填写一个适当的条件: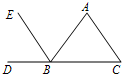 17、如图,请你填写一个适当的条件:
17、如图,请你填写一个适当的条件: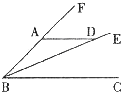 25、如图,射线BE在∠FBC的内部,点A、D分别在射线BF、BE上.请你填写一个适当的条件:
25、如图,射线BE在∠FBC的内部,点A、D分别在射线BF、BE上.请你填写一个适当的条件: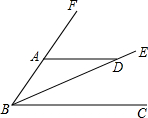 如图,①请你填写一个适当的条件:
如图,①请你填写一个适当的条件: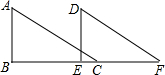 如图,Rt△ABC中,∠ABC=90°,将其沿直角边BC所在的直线向右平移得到△DEF,请你填写一个你认为正确的结论
如图,Rt△ABC中,∠ABC=90°,将其沿直角边BC所在的直线向右平移得到△DEF,请你填写一个你认为正确的结论