题目内容
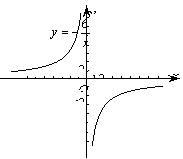
正方形ABCD的顶点A在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E,过点B作BF⊥MN于点F.
(1)如图1,当O、B两点均在直线MN上方时,求证:AF+BF=2OE
(2)当正方形ABCD绕点A顺时针旋转至图2时.线段 AF,BF与OE具有什么数量关系?并说明理由.
(3)当运动到图3的位置时,线段AF、BF、OE之间又有怎样的数量关系?请直接写出你的猜想

窗体顶端






窗体底端
 提示过D点作DH垂直MN。
提示过D点作DH垂直MN。
可证得 △DAH
△DAH △AFB.............2分
△AFB.............2分
证得AF+BF=2OE…………….5分

(2)提示过B点作BG垂直OE于G.则四边形EFBG是矩形。
则FB=EG,GB=EF.
可证得△OAE △BOG…………8分
△BOG…………8分
则AE=OG,OE=GB=EF.
可证得AF-BF=AE+EF-BF=OG+EF-BF=2OE…………10分
(3)BF-AF=2OE………………….14分

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 ,则∠A=________.
,则∠A=________.
 的最简公分母为_________.
的最简公分母为_________.

 B.
B. C.
C. D.
D.
 中,一次函数
中,一次函数 和反比例函数
和反比例函数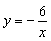 的图象都经过点
的图象都经过点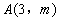 。
。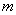 的值和一次函数的表达式;
的值和一次函数的表达式; 在双曲线
在双曲线