题目内容
已知等式(x-4)m=x-4,且m≠1,则x=________.
4
分析:首先把方程整理成(m-1)x=4m-4,再根据等式的性质2,两边同时除以m-1即可.
解答:(x-4)m=x-4,
整理得:(m-1)x=4m-4,
∵m≠1,
∴m-1≠0,
根据等式的性质2,两边同时除以m-1得:
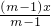 =
=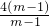 ,
,
即:x=4.
故答案为:4.
点评:此题主要考查了等式的性质,关键是掌握等式的性质:
性质1、等式两边加同一个数(或式子)结果仍得等式;
性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.
分析:首先把方程整理成(m-1)x=4m-4,再根据等式的性质2,两边同时除以m-1即可.
解答:(x-4)m=x-4,
整理得:(m-1)x=4m-4,
∵m≠1,
∴m-1≠0,
根据等式的性质2,两边同时除以m-1得:
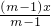 =
=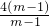 ,
,即:x=4.
故答案为:4.
点评:此题主要考查了等式的性质,关键是掌握等式的性质:
性质1、等式两边加同一个数(或式子)结果仍得等式;
性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知等式ab+a=2002,ab+b=2001,如果a和b分别代表一个整数,那么a-b的值是( )
| A、2 | B、1 | C、2000 | D、0 |
