题目内容
在直角坐标系中,A(-3,4),B(-1,-2),O为原点,求△AOB的面积.
 解:设过点A、B的直线为y=kx+b(k≠0),点D的坐标为(x,0).则根据题意,得
解:设过点A、B的直线为y=kx+b(k≠0),点D的坐标为(x,0).则根据题意,得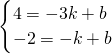 ,
,解得,
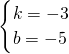 ,
,则0=-3x-5,
解得,x=-
 ,
,∴OD=
 .
.分别过A、B两点作垂线,垂足分别为C、E,
则S△AOD=
 OD•AC=
OD•AC= ×
× ×4=
×4= ;
;S△OBD=
 OD•BE=
OD•BE= ×
× ×2=
×2= ,
,∴S△AOB=S△AOD+S△OBD=
 +
+ =5.
=5.分析:分别过A、B两点向x轴作垂线,利用三角形的面积公式求解即可.
点评:求不规则三角形的面积,往往采用割补法,变成几个规则图形的面积的和或差.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 在直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依此连接起来形成一个图案.
在直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依此连接起来形成一个图案. 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,