Question

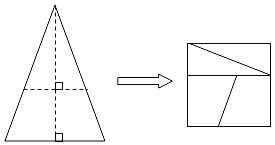
【题目】如图，将等腰三角形纸片沿图中虚线剪成四块图形，用这四块图形进行拼接，恰能拼成一个没有缝隙的正方形，则正方形的边长与等腰三角形的底边长的比为(　　)

A.B.C.D.

Answer 1

【答案】B

【解析】

如图，等腰三角形纸片沿图中虚线剪成四块图形，能拼成一个没有缝隙的正方形和矩形，根据题意得(a+b)2=b(b+a+b)，设a=1，求出b=，进而求出正方形的边长与等腰三角形的底边长的比．

解：如图，等腰三角形纸片沿图中虚线剪成四块图形，能拼成一个没有缝隙的正方形和矩形，

设a=1，

根据题意，得

(a+b)2=b(b+a+b)，

∵a=1，

∴b2﹣b﹣1=0，

解得b (负值舍去)，

∴b=，

∴正方形的边长与等腰三角形的底边长的比为：

(a+b)：2b=．

故选：B．