题目内容
 有一圆柱,它的高等于8cm,底面直径等于4cm(π=3)在圆柱下底面的A点有一蚂蚁,它想吃到上底面与A相对的B点处的食物,求需要爬行的最短路程.
有一圆柱,它的高等于8cm,底面直径等于4cm(π=3)在圆柱下底面的A点有一蚂蚁,它想吃到上底面与A相对的B点处的食物,求需要爬行的最短路程.分析:首先将此圆柱展成平面图,根据两点间线段最短,可得AB最短,由勾股定理即可求得需要爬行的最短路程.
解答: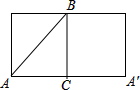 解:将此圆柱展成平面图得:
解:将此圆柱展成平面图得:
∵有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),
∴BC=8cm,AC=
AA′=
×4π=6(cm),
∴AB=
=10(cm).
∴需要爬行的最短路程为10cm.
 解:将此圆柱展成平面图得:
解:将此圆柱展成平面图得:∵有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),
∴BC=8cm,AC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| AC2+BC2 |
∴需要爬行的最短路程为10cm.
点评:此题考查了最短路径问题.此题难度适中,注意将立体图形展成平面图形是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 30、如图:有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约( )
30、如图:有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约( ) 有一圆柱,它的高等于8cm,底面直径等于4cm(π=3)在圆柱下底面的A点有一蚂蚁,它想吃到上底面与A相对的B点处的食物,求需要爬行的最短路程.
有一圆柱,它的高等于8cm,底面直径等于4cm(π=3)在圆柱下底面的A点有一蚂蚁,它想吃到上底面与A相对的B点处的食物,求需要爬行的最短路程.