题目内容
在△ABC中,点D是AB上一点,△ADC与△BDC都是等腰三角形且底边分别为AC,BC,则∠ACB的度数为
- A.60°
- B.72°
- C.90°
- D.120°
C
分析:根据三角形内角和定理可得∠A+∠B+∠ACB=180°,再根据等腰三角形的性质可得∠A+∠B=∠ACB,则可求∠ACB的度数.
解答: 解:如图:
解:如图:
∵△ADC与△BDC是等腰三角形且底边分别为AC、BC,
∴∠A=∠ACD,∠B=∠DCB,
∴∠A+∠B=∠ACB,
∵∠A+∠B+∠ACB=180°,
∴∠ACB=90°.
故选C.
点评:考查了等腰三角形的性质和三角形内角和定理,得到∠A+∠B=∠ACB是解题的关键.
分析:根据三角形内角和定理可得∠A+∠B+∠ACB=180°,再根据等腰三角形的性质可得∠A+∠B=∠ACB,则可求∠ACB的度数.
解答:
 解:如图:
解:如图:∵△ADC与△BDC是等腰三角形且底边分别为AC、BC,
∴∠A=∠ACD,∠B=∠DCB,
∴∠A+∠B=∠ACB,
∵∠A+∠B+∠ACB=180°,
∴∠ACB=90°.
故选C.
点评:考查了等腰三角形的性质和三角形内角和定理,得到∠A+∠B=∠ACB是解题的关键.

练习册系列答案
相关题目
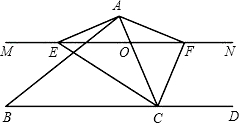 如图,在△ABC中,点O是AC边上的一个动点(点O不与A、C两点重合),过点O作直线MN∥BC,直线MN与∠BCA的平分线相交于点E,与∠DCA(△ABC的外角)的平分线相交于点F.
如图,在△ABC中,点O是AC边上的一个动点(点O不与A、C两点重合),过点O作直线MN∥BC,直线MN与∠BCA的平分线相交于点E,与∠DCA(△ABC的外角)的平分线相交于点F.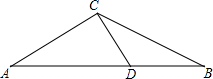
 5、如图,在△ABC中,点O是∠ABC与∠ACB的角平分线的交点,若∠BAC=80°,则∠BOC=( )
5、如图,在△ABC中,点O是∠ABC与∠ACB的角平分线的交点,若∠BAC=80°,则∠BOC=( ) 7、在△ABC中,点O是△ABC的内心,连接OB、OC,过点O作EF∥BC分别交AB、AC于点E、F,已知BC=a (a是常数),设△ABC的周长为y,△AEF的周长为x,在下列图象中,大致表示y与x之间的函数关系的是( )
7、在△ABC中,点O是△ABC的内心,连接OB、OC,过点O作EF∥BC分别交AB、AC于点E、F,已知BC=a (a是常数),设△ABC的周长为y,△AEF的周长为x,在下列图象中,大致表示y与x之间的函数关系的是( ) (2011•青浦区一模)如图,在△ABC中,点D是AB上的一点,过点D作DE∥BC交边AC于点E,过点E作EF∥DC交AD于点F.已知AD=2
(2011•青浦区一模)如图,在△ABC中,点D是AB上的一点,过点D作DE∥BC交边AC于点E,过点E作EF∥DC交AD于点F.已知AD=2