题目内容
 如图1,边长为a的大正方形中有一个边长为b的小正方形,若将图1中的阴影部分拼成一个长方形如图2,比较图1和图2中的阴影部分的面积,
如图1,边长为a的大正方形中有一个边长为b的小正方形,若将图1中的阴影部分拼成一个长方形如图2,比较图1和图2中的阴影部分的面积,(1)你能得到用于因式分解的公式是什么?简要写明理由.
(2)将图(1)中的阴影部分适当剪切,可拼成与图2不同的几何图形来验证此公式,请你画出剪切线及拼成的图形.
分析:(1)分别求出图1的大正方形及小正方形的面积,作差即可得出阴影部分的面积;图2所示的长方形的长和宽分别为(a+b)、(a-b),由此可计算出面积;根据阴影部分的面积相等可得出平方差公式.
(2)作一个底为(a+b)、高为(a-b)的平行四边形即可.
(2)作一个底为(a+b)、高为(a-b)的平行四边形即可.
解答:解:(1)大正方形的面积为a2,小正方形的面积为b2,
故图1阴影部分的面积值为a2-b2.
长方形的长和宽分别为(a+b)、(a-b),
故图2重拼的长方形的面积为(a+b)(a-b).
则a2-b2=(a+b)(a-b),可以验证平方差公式,这也是平方差公式的几何意义.
(2)如图3所示:

故图1阴影部分的面积值为a2-b2.
长方形的长和宽分别为(a+b)、(a-b),
故图2重拼的长方形的面积为(a+b)(a-b).
则a2-b2=(a+b)(a-b),可以验证平方差公式,这也是平方差公式的几何意义.
(2)如图3所示:

点评:本题考查了平方差公式的几何背景,注意几次分割后边的变化情况是关键,属于基础题.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
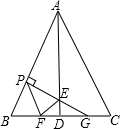 如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过P点作PF∥AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设BP=x.
如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过P点作PF∥AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设BP=x.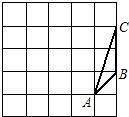 如图,由边长为1的25个小正方形组成的网格上有一个△ABC.
如图,由边长为1的25个小正方形组成的网格上有一个△ABC. (2013•百色)如图,在边长为10cm的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为
(2013•百色)如图,在边长为10cm的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为 (2012•无锡)如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
(2012•无锡)如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm). 设平移的距离为x(cm),两个三角形重叠部分(阴影四边形)的面积为S(cm2).
设平移的距离为x(cm),两个三角形重叠部分(阴影四边形)的面积为S(cm2).