题目内容
11.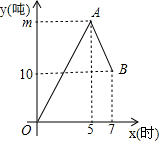 某仓库有甲、乙、丙三辆运货车,在满载的情况下,甲车每小时可运货6吨,乙车每小时可运货10吨,某天只有乙车负责进货,甲车和丙车负责出货.如图是从早晨上班开始库存量y(吨)与时间x(时)之间的函数图象,OA段表示甲、乙两车一起工作,AB段表示乙、丙两车一起工作,且在工作期间,每辆车都是满载的.
某仓库有甲、乙、丙三辆运货车,在满载的情况下,甲车每小时可运货6吨,乙车每小时可运货10吨,某天只有乙车负责进货,甲车和丙车负责出货.如图是从早晨上班开始库存量y(吨)与时间x(时)之间的函数图象,OA段表示甲、乙两车一起工作,AB段表示乙、丙两车一起工作,且在工作期间,每辆车都是满载的.(1)m=20.
(2)在满载的情况下,丙车每小时可运货15吨.
(3)求AB段中库存量y(吨)与时间x(时)之间的函数表达式.
分析 (1)由图可知:甲、乙两车一起工作,每小时进货10-6=4吨,由此求得5小时的进货量得出m的数值即可;
(2)由图可知:乙、丙两车一起工作,7-5=2小时出货20-10=10吨,每小时出货5吨,由此得出丙车每小时可运货10+5=15吨;
(3)设出一次函数解析式,代入点A、B求得答案即可.
解答 解:(1)由图可知:甲、乙两车一起工作,每小时进货10-6=4吨,
则m=4×5=20;
(2)由图可知:乙、丙两车一起工作,
7-5=2小时出货20-10=10吨,
10+10÷2=15吨
丙车每小时可运货15吨;
(3)由(1)(2)可知A(5,20),B(7,10),
设AB段中库存量y(吨)与时间x(时)之间的函数表达式为y=kx+b,
则$\left\{\begin{array}{l}{5k+b=20}\\{7k+b=10}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-5}\\{b=45}\end{array}\right.$,
即AB段的函数表达式为y=-5x+45.
点评 此题考查一次函数的实际运用,待定系数法求函数解析式,解答时认真分析函数图象的数据意义是关键.

练习册系列答案
相关题目
2.不等式组$\left\{\begin{array}{l}x≤-2\\ x-2>1\end{array}\right.$的解集是( )
| A. | x≤-2 | B. | x>3 | C. | 3<x≤-2 | D. | 无解 |
19. 如图,在平面直角坐标系中,等腰直角三角形ABC的顶点B与原点O重合,顶点A、C分别在y轴、x轴的正半轴上,将Rt△ABC沿直线y=2x向上平移得到Rt△A′B′C′,纵坐标为4,若AB=BC=3,则点A′的坐标为( )
如图,在平面直角坐标系中,等腰直角三角形ABC的顶点B与原点O重合,顶点A、C分别在y轴、x轴的正半轴上,将Rt△ABC沿直线y=2x向上平移得到Rt△A′B′C′,纵坐标为4,若AB=BC=3,则点A′的坐标为( )
 如图,在平面直角坐标系中,等腰直角三角形ABC的顶点B与原点O重合,顶点A、C分别在y轴、x轴的正半轴上,将Rt△ABC沿直线y=2x向上平移得到Rt△A′B′C′,纵坐标为4,若AB=BC=3,则点A′的坐标为( )
如图,在平面直角坐标系中,等腰直角三角形ABC的顶点B与原点O重合,顶点A、C分别在y轴、x轴的正半轴上,将Rt△ABC沿直线y=2x向上平移得到Rt△A′B′C′,纵坐标为4,若AB=BC=3,则点A′的坐标为( )| A. | (3,7) | B. | (2,7) | C. | (3,5) | D. | (2,5) |
3.已知100a=8,10b=125,则(2a)2×2b的值为( )
| A. | 8 | B. | $\frac{1}{8}$ | C. | 125 | D. | -125 |
20.计算4-(-4)0的结果是( )
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
