Question

【题目】如图，⊙的半径为5，AB为直径，C是圆周上一点。

（1）求∠ACB的度数。

（2）若AC＝AO，求阴影部分的面积(用含的代数式表示).

（3）当C点在圆周上移动时，AC、BC、AB三条线段的长度之间存在着恒定不变的关系，请你写出一种这样的关系，并说明你的理由.

Answer 1

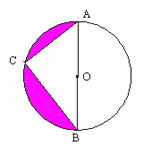
【答案】（1）∠ACB＝90°；（2）；（3）AC+BC＞AB，或者.

【解析】

（1）直接根据圆周角定理的推论解答即可；

（2）根据S阴影=S半圆-S△ABC计算即可；

（3）根据三角形三条边的关系或勾股定理解答即可.

解：（1）∵AB是⊙的直径，∴∠ACB＝90°；

　（2）∵AC＝AO＝5，∠ACB＝90°，

∴BC＝，

∴S阴影=S半圆-S△ABC＝

（3）由三角形两边之和大于第三边，得AC+BC＞AB；

或者，由勾股定理，得上移动时.