Question

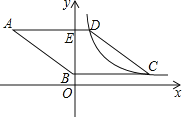
【题目】 梯形ABCD中，AD∥BC，请用尺规作图并解决问题．

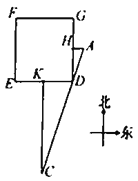
（1）作AB中点E，连接DE并延长交射线CB于点F，在DF的下方作∠FDG＝∠ADE，边DG交BC于点G，连接EG；

（2）试判断EG与DF的位置关系，并说明理由．

Answer 1

【答案】（1）如图所示，见解析；（2）见解析.

【解析】

(1)作出线段AB的垂直平分线，进而得出AB的中点E，再作∠FDG=∠ADE，求出即可；

(2)首先得出△ADE≌△BFE(AAS)，进而求出EF=DE，然后证明DG=FG，利用等腰三角形的性质得出答案．

(1)如图所示：

(2)∵AD∥BC，

∴∠ADE＝∠F，

在△ADE和△BFE中，

，

∴△ADE≌△BFE(AAS)，

∴EF＝DE，

又∵∠ADE＝∠FDG，

∴∠F＝∠FDG，

∴DG＝FG，

∴EG⊥DF．