题目内容
已知x可以为任意值，则|2x-1|+|x+2|的最小值是
- A.
- B.5
- C.3
- D.
A
分析：根据绝对值的性质，分别讨论2x-1，x+2与0之间的关系，算出结果，比较得出最后结果．
解答：①由2x-1＞0，x+2＞0得，x＞
，
此时，|2x-1|+|x+2|=3x+1＞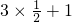
即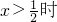
，|2x-1|+|x+2|
；
②由2x-1＜0，x+2＜0得，x＜-2，
此时，|2x-1|+|x+2|=-3x-1＞-3×（-2）-1，
即 x＜-2时，|2x-1|+|x+2|＞5；
③由2x-1≤0，x+2≥0得，-2≤x≤，
此时，|2x-1|+|x+2|=3-x，
-2≤x≤时，3-≤x≤3-（-2），
即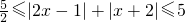
，
所以，当x=时，|2x-1|+|x+2|最小，为；
由2x-1＞0，x+2＜0得，x无解；
综上可知，当x=，|2x-1|+|x+2|的值最小为．
故选A．
点评：本题主要考查了绝对值的性质：正数和0的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0．
分析：根据绝对值的性质，分别讨论2x-1，x+2与0之间的关系，算出结果，比较得出最后结果．
解答：①由2x-1＞0，x+2＞0得，x＞
，此时，|2x-1|+|x+2|=3x+1＞
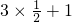
即
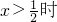，|2x-1|+|x+2|；②由2x-1＜0，x+2＜0得，x＜-2，
此时，|2x-1|+|x+2|=-3x-1＞-3×（-2）-1，
即 x＜-2时，|2x-1|+|x+2|＞5；
③由2x-1≤0，x+2≥0得，-2≤x≤
，此时，|2x-1|+|x+2|=3-x，
-2≤x≤
时，3-≤x≤3-（-2），即
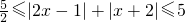，所以，当x=
时，|2x-1|+|x+2|最小，为；由2x-1＞0，x+2＜0得，x无解；
综上可知，当x=
，|2x-1|+|x+2|的值最小为．故选A．
点评：本题主要考查了绝对值的性质：正数和0的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0．
练习册系列答案
相关题目
已知x可以为任意值，则|2x-1|+|x+2|的最小值是（ ）
A、
| ||
| B、5 | ||
| C、3 | ||
D、
|
九年义务教育三年制初级中学教科书代数第三册中，有以下几段文字：“对于坐标平面内任意一点M，都有唯一的一对有序实数（x，y）和它对应；对于任意一对有序实数（x，y），在坐标平面内都有唯一的一点M和它对应，也就是说，坐标平面内的点与有序实数对是一一对应的．”“一般地，对于一个函数，如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标，在坐标平面内描出相应的点，这些点所组成的图形，就是这个函数的图象．”“实际上，所有一次函数的图象都是一条直线．”“因为两点确定一条直线，所以画一次函数的图象时，只要先描出两点，再连成直线，就可以了．”由此可知：满足函数关系式的有序实数对所对应的点，一定在这个函数的图象上；反之，函数图象上的点的坐标，一定满足这个函数的关系式．另外，已知直线上两点的坐标，便可求出这条直线所对应的一次函数的解析式．