题目内容
如图，已知∠AOB=30°，在OA边上有一点C，OC长为4cm，若以C为圆心，2cm长为半径画一个圆⊙C，则⊙C与OB边的位置关系是（ ）| A、相离 | B、相切 | C、相交 | D、内切 |
分析：判断⊙C与OB边的位置关系，关键是比较点C到直线OB的距离与半径的大小关系．
解答：
解：过C点作CD⊥OB，垂足为D，
在Rt△OCD中，∠AOB=30°，OC=4，
∴CD=
OC=2，又圆的半径为2，
∴⊙C与OB相切．
故选B．
解：过C点作CD⊥OB，垂足为D，在Rt△OCD中，∠AOB=30°，OC=4，
∴CD=
| 1 |
| 2 |
∴⊙C与OB相切．
故选B．
点评：本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．
练习册系列答案
相关题目
如图，已知∠AOB是直角，∠AOC是锐角，ON平分∠AOC，OM平分∠BOC，则∠MON是（ ）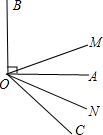
| A、45° | ||
B、45°+
| ||
C、60°-
| ||
| D、不能计算 |
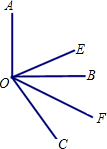如图，已知∠AOB是直角，∠BOC=60°，OE平分∠AOC，OF平分∠BOC．
尺规作图：
如图，已知∠AOB=x（0°＜x＜180°），OC平分∠AOB，点N为OB上一个定点．通过画图可以知道：当∠AOB=45°时，在射线OC上存在点P，使△ONP成为等腰三角形，且符合条件的点有三个，即P1（顶点为P2），P2（顶点为0），P3（顶点为N）．