题目内容
已知△ABC的周长为P,内切圆的半径r,求△ABC的面积.
考点:三角形的内切圆与内心
专题:
分析:O做OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,连接OB、OA、OC,得出OD=OE=OF,根据S△ABC=S△OAB+S△OBC+S△OAC,求出即可.
解答: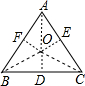 解:过O做OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,连接OB、OA、OC,
解:过O做OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,连接OB、OA、OC,
则OD=OE=OF,
则S△ABC=S△OAB+S△OBC+S△OAC,
所以S△ABC=
×AB×OF+
×BC×OD+
×AC×OE=
(AB+BC+AC)×r=
pr.
 解:过O做OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,连接OB、OA、OC,
解:过O做OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,连接OB、OA、OC,则OD=OE=OF,
则S△ABC=S△OAB+S△OBC+S△OAC,
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形的内心和内切圆三角形的面积的应用,能求出S△ABC=
(AB+BC+AC)r是解此题的关键.
| 1 |
| 2 |

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 美化城市、改善人们的居住环境已成为城市建设的一项重要内容.某区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加,根据图中所提供的信息,下列说法错误的是( )
美化城市、改善人们的居住环境已成为城市建设的一项重要内容.某区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加,根据图中所提供的信息,下列说法错误的是( )| A、2009年该区的绿地面积为420公顷 |
| B、2011年的绿地面积增长最快 |
| C、从2009年到2012年,每年绿地面积的增长率都在增长 |
| D、从2009年到2012年,每年的绿地面积都在增长 |
 如图所示,将直角边长为6
如图所示,将直角边长为6 如图,⊙O的直径是4cm,C是
如图,⊙O的直径是4cm,C是