题目内容
已知a,b,c为实数,且a+b+| -1|=4
-1|=4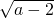 +2
+2 -4,求:a+2b-3c的值.
-4,求:a+2b-3c的值.
解:移项得:a+b+| -1|-4
-1|-4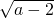 -2
-2 +4=0,
+4=0,
配方,得:(a-2-4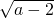 +4)+(b+1-2
+4)+(b+1-2 +1)+|
+1)+| -1|=0,
-1|=0,
即(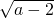 -2)2+(
-2)2+( -1)2+|
-1)2+| -1|=0,
-1|=0,
根据非负数的性质得,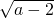 =2,
=2, =1,
=1, =1,
=1,
解得,a=6,b=0,c=2,
所以a+2b-3c=6+2×0-3×2=0.
分析:对所给等式进行移项得:a+b+| -1|-4
-1|-4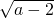 -2
-2 +4=0,根据要求凑完全平方式:(a-2-4
+4=0,根据要求凑完全平方式:(a-2-4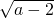 +4)+(b+1-2
+4)+(b+1-2 +1)+|
+1)+| -1|=0,即(
-1|=0,即(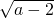 -2)2+(
-2)2+( -1)2+|
-1)2+| -1|=0,根据非负数的性质,可分别解出a、b、c的值,进而求出所求代数式的值.
-1|=0,根据非负数的性质,可分别解出a、b、c的值,进而求出所求代数式的值.
点评:本题考查了学生配方的能力,对式子适当变形是解题的关键,注意变形时不能改变式子的值.
 -1|-4
-1|-4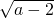 -2
-2 +4=0,
+4=0,配方,得:(a-2-4
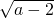 +4)+(b+1-2
+4)+(b+1-2 +1)+|
+1)+| -1|=0,
-1|=0,即(
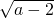 -2)2+(
-2)2+( -1)2+|
-1)2+| -1|=0,
-1|=0,根据非负数的性质得,
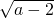 =2,
=2, =1,
=1, =1,
=1,解得,a=6,b=0,c=2,
所以a+2b-3c=6+2×0-3×2=0.
分析:对所给等式进行移项得:a+b+|
 -1|-4
-1|-4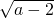 -2
-2 +4=0,根据要求凑完全平方式:(a-2-4
+4=0,根据要求凑完全平方式:(a-2-4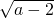 +4)+(b+1-2
+4)+(b+1-2 +1)+|
+1)+| -1|=0,即(
-1|=0,即(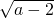 -2)2+(
-2)2+( -1)2+|
-1)2+| -1|=0,根据非负数的性质,可分别解出a、b、c的值,进而求出所求代数式的值.
-1|=0,根据非负数的性质,可分别解出a、b、c的值,进而求出所求代数式的值.点评:本题考查了学生配方的能力,对式子适当变形是解题的关键,注意变形时不能改变式子的值.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目