题目内容
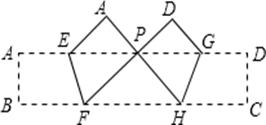
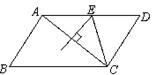
(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?

(1)相等;(2) 平方米.
平方米.
 平方米.
平方米.试题分析:(1)过点
 作
作 于
于 ,过点
,过点 作
作 交
交 延长线于
延长线于 ,可得
,可得
 ,再结合正方形的性质,同角的补角相等可得△ACM≌△AGN,即可得到CM=GN,根据等底等高的三角形的面积相等,即可得到结果;
,再结合正方形的性质,同角的补角相等可得△ACM≌△AGN,即可得到CM=GN,根据等底等高的三角形的面积相等,即可得到结果;(2)由(1)知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和,即得结果.
(1)
 与
与 面积相等
面积相等过点
 作
作 于
于 ,过点
,过点 作
作 交
交 延长线于
延长线于 ,
,则


 四边形
四边形 和四边形
和四边形 都是正方形
都是正方形





(2) 由(1)知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和
∴这条小路的面积为
 平方米.
平方米.点评:解答本题的关键是掌握正方形的四条边相等,四个角都是直角,同角的补角相等,等底等高的两个三角形的面积相等.

练习册系列答案
相关题目
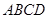 沿
沿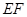 ,
,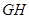 同时折叠,
同时折叠,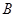 、
、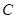 两点恰好都落在
两点恰好都落在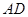 边的
边的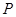 点处,若
点处,若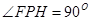 ,
,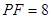 ,
,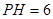 ,则长方形
,则长方形