题目内容
如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为 .


【解析】
试题分析:过点B作BE⊥x轴于点E,B′作B′F⊥x轴于点F,所以BE∥B′F,所以△ABE∽△AB′F,所以 ,
,

因为△AB′O′是△ABO关于的A的位似图形,所以△ABO∽△AB′O′,所以
因为O′的坐标为(-1,0),点A、B的坐标分别为(3,0)、(2,-3),所以AE=1,EO=2,BE=3,
所以 =
= =
= , 所以
, 所以 =
= =
= ,所以
,所以 =
= ,所以AF=
,所以AF= ,所以EF=
,所以EF= ,所以FO=2-
,所以FO=2- =
= ,
,
因为 =
= ,解得:B′F=4,则点B′的坐标为:(
,解得:B′F=4,则点B′的坐标为:( ,-4).
,-4).
考点:1.位似图形;2.点的坐标..

练习册系列答案
相关题目
(本题10分)已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)点A表示的数为 ,点B表示的数为 ,点C表示的数为 .
(2)用含t的代数式表示P到点A和点C的距离: PA= ,PC= .
(3)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.①在点Q向点C运动过程中,能否追上点P?若能,请求出点Q运动几秒追上.②在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.

 与
与 的值相等,则已知程方组
的值相等,则已知程方组 中
中 的值是( ).
的值是( ). (C)
(C) (D)
(D)

 (需用配方法解)
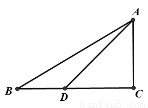
(需用配方法解) , ∠ADC=45°,DC=6,求BD的长.
, ∠ADC=45°,DC=6,求BD的长.