题目内容
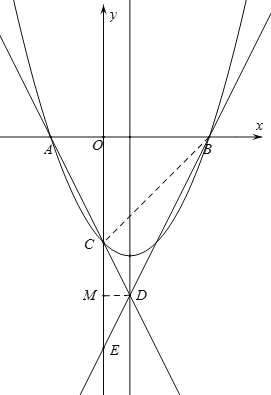
【题目】已知二次函数![]() (a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(1)求C点坐标,并判断b的正负性;
(2)设这个二次函数的图像的对称轴与直线AC交于点D,已知DC:CA=1:2,直线BD与y轴交于点E,连接BC,
①若△BCE的面积为8,求二次函数的解析式;
②若△BCD为锐角三角形,请直接写出OA的取值范围.

【答案】(1)b<0;(2)①![]() ;②
;②![]()
【解析】
(1)把x=0代入![]() ,即可求得点C坐标,根据 OA<OB,可知
,即可求得点C坐标,根据 OA<OB,可知![]() ,由a>0即可求得b<0;
,由a>0即可求得b<0;
(2)①过点D作DM⊥y轴,垂足为M,则有![]() ,由此可得
,由此可得![]() ,设A(-2m,0)m>0,则AO=2m,DM=m,继而可得D(m,-6),B(4m,0),AB=6m, BN=3m,再由DN//OE,可得△BND∽△BOE,继而根据相似三角形的性质可得OE=8,再根据
,设A(-2m,0)m>0,则AO=2m,DM=m,继而可得D(m,-6),B(4m,0),AB=6m, BN=3m,再由DN//OE,可得△BND∽△BOE,继而根据相似三角形的性质可得OE=8,再根据![]() ,可求得
,可求得![]() ,由此可得A(-2,0),B(4,0),设
,由此可得A(-2,0),B(4,0),设![]() ,继而可得C(0,-8a),再根据C点(0,-4)可求得a值,即可求得答案;
,继而可得C(0,-8a),再根据C点(0,-4)可求得a值,即可求得答案;
②由①易知:B(4m,0),C(0,-4),D(m,-6),∠CBD一定为锐角,利用勾股定理求得![]() ,然后分两种情况进行讨论即可得.
,然后分两种情况进行讨论即可得.
(1)当x=0时,![]() =-4,
=-4,
∴C(0,-4),
∵ OA<OB,∴对称轴在y轴右侧,即![]() ,
,
∵a>0,∴b<0;
(2)①过点D作DM⊥y轴,垂足为M,则有DM//OA,
∴△DCM∽△ACO,
∴![]() ,
,
∴![]() ,
,
设A(-2m,0)m>0,则AO=2m,DM=m,
∵OC=4,∴CM=2,
∴D(m,-6),B(4m,0),AB=6m, BN=3m,
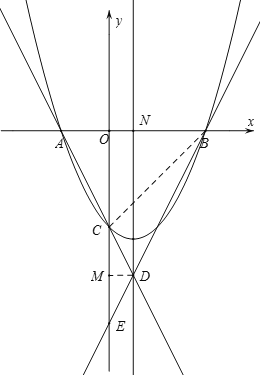
∵DN//OE,
∴△BND∽△BOE,
∴![]() ,
,
即![]() ,
,
∴OE=8,
∴CE=OE-OC=4,
∴![]() ,
,
∴![]() ,
,
∴A(-2,0),B(4,0),
设![]() ,
,
即![]() ,
,
令x=0,则y=-8a,
∴C(0,-8a),
∴-8a=-4,
∴a=![]() ,
,
∴![]() ;
;
②由①易知:B(4m,0),C(0,-4),D(m,-6),∠CBD一定为锐角,
由勾股定理可得:![]() ,
,
当∠CDB为锐角时,![]() ,
,
![]() ,
,
解得![]() ;
;
当∠BCD为锐角时,![]() ,
,
![]() ,
,
解得![]() ,
,
综上:![]() ,
,
∴![]() ,
,
∴![]() .
.