Question

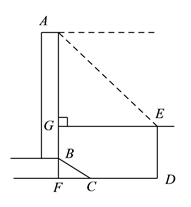
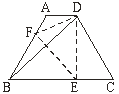
【题目】如图，等腰梯形ABCD中，AD∥BC，∠DBC=45°，翻折梯形ABCD，使点B重合于点D，折痕分别交边AB、BC于点F、E，若AD=2，BC=8.则(1)BE的长为_________. (2)∠CDE的正切值为________.

Answer 1

【答案】BE=5； tan∠CDE=

【解析】

（1）由轴对称的性质可以得出△BFE≌△DFE，从而得出DE=BE，由∠DBC=45°可以得出∠BED=90°，过A作AG⊥BC于G，可以求出BG=3，可以求出BE的值．
（2）根据tan∠CDE=，由（1）的结论可以求出其值．

（1）由题意得△BFE≌△DFE，

∴DE=BE.

又∵在△BDE中，∠DBE=45°，

∴∠BDE=∠DBE=45°，

∴∠BED=90°，即DE⊥BC.

∵在等腰梯形ABCD中，AD=2，BC=8，

过A作AG⊥BC于G，

∵四边形AGED是矩形．
∴AD=GE=2，AG=DE．
∵四边形ABCD是等腰梯形，
∴AB=CD，
∵∠AGB=∠DEC=90°
Rt△ABG和Rt△DCE中，

∴Rt△ABG≌Rt△DCE（HL），
∴BG=EC=3．
∴BE=5

(2)由(1)得DE=BE=5，

在△DEC中，∠DEC=90°，DE=5，EC=3，

∴tan∠CDE==

故答案为：(1) BE=5； (2) tan∠CDE=