题目内容
【题目】已知抛物线![]() 的顶点是
的顶点是![]() ,抛物线
,抛物线![]() 的顶点是
的顶点是![]() .
.
(1)判断点![]() 是否在抛物线
是否在抛物线![]() 上,为什么?
上,为什么?
(2)如果抛物线![]() 经过点
经过点![]() .
.
①求![]() 的值;
的值;
②直线![]() 与
与![]() 分别交于点
分别交于点![]() (点
(点![]() 在
在![]() 的左边),直线
的左边),直线![]() 与
与![]() 分别交于点
分别交于点![]() (点
(点![]() 在
在![]() 的左边)是否存在
的左边)是否存在![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 值;若不存在,说明理由.
值;若不存在,说明理由.
③在②的条件下,当![]() 为何值时, 抛物线
为何值时, 抛物线![]() 和
和![]() 中
中![]() 都随
都随![]() 的增大而增大?
的增大而增大?

【答案】(1)点![]() 在抛物线
在抛物线![]() 上,理由见解析;(2)①
上,理由见解析;(2)①![]() ;②
;②![]() ;③当
;③当![]() 时,抛物线
时,抛物线![]() 和
和![]() 中
中![]() 都随
都随![]() 的增大而增大.
的增大而增大.
【解析】(1)先求顶点A的坐标,再将A的坐标代入![]() ,可判断A再抛物线上;(2)①把点
,可判断A再抛物线上;(2)①把点![]() (1,0)代入
(1,0)代入![]() ,可求a; ②结合图象进行分析,求出直线与抛物线的交点坐标,可得到
,可求a; ②结合图象进行分析,求出直线与抛物线的交点坐标,可得到![]() 的长度,
的长度,
根据![]() ,可求出t;
,可求出t;
③分两种情况当![]() 时, y都随
时, y都随![]() 的增大而增大;当
的增大而增大;当![]() 都随
都随![]() 的增大而增大.
的增大而增大.
解:(1) 点![]() 在抛物线
在抛物线![]() 上.
上.
理由:∵![]() (
(![]() ).当
).当![]() 时,
时,![]() -2(
-2(![]() .
.
∴![]() 在抛物线
在抛物线![]() 上.
上.
(2)①点![]() (1,0).
(1,0).
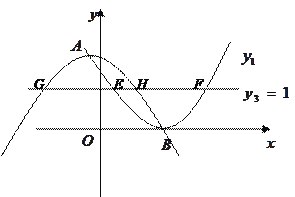
∵![]() 经过点
经过点![]() (1,0).∴
(1,0).∴![]()
②由![]()
解得![]()
∴![]()
∵![]() 解得
解得![]()
∴![]()
![]()
∵![]() ∴
∴![]() ,
,![]()
③当![]() 时,抛物线
时,抛物线![]() 和
和![]() 中
中![]() 都随
都随![]() 的增大而增大.
的增大而增大.

当![]() 使得抛物线
使得抛物线![]() 和
和![]() 中
中![]() 都随
都随![]() 的增大而增大.
的增大而增大.

练习册系列答案
相关题目