题目内容
铁板甲形状为等腰三角形,其顶角为120°,腰长16cm,铁板乙形状为直角梯形,两底分别为4cm、12cm,且有一个角为45°,现在我们把它们任意翻转,分别试图从一个直径为8.2cm的圆洞中穿过,结果
- A.甲、乙都能穿过
- B.甲、乙都不能穿过
- C.甲能而乙不能穿过
- D.甲不能而乙能穿过
A
分析:把一边水平放置,看最高顶点到这边所在直线的距离是否小于圆洞的直径即可.
解答: 解:∵等腰三角形,顶角为120°,
解:∵等腰三角形,顶角为120°,
∴底角为(180°-120°)÷2=30°,
∴AD= =
=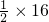 =8,
=8,
∴AD<8.2cm,
∴甲能穿过圆洞.

在梯形ABCD中,作DE⊥BC于E,
∵AD∥BC,AB⊥BC,AD=4cm,BC=12cm,
∴BE=AD=4,
∴CE=BC-BE=12-4=8,
∵∠C=45°,
∴DE=CE=8<8.2,
所以乙能穿过圆洞.
故选A.
点评:考查几何图形与圆的关系;用到的知识点为:一个多边形能否穿过圆洞,只要看是否存在距离某一边所在直线最远的顶点到这条直线的距离小于圆洞的直径.
分析:把一边水平放置,看最高顶点到这边所在直线的距离是否小于圆洞的直径即可.
解答:
 解:∵等腰三角形,顶角为120°,
解:∵等腰三角形,顶角为120°,∴底角为(180°-120°)÷2=30°,
∴AD=
 =
=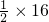 =8,
=8,∴AD<8.2cm,
∴甲能穿过圆洞.

在梯形ABCD中,作DE⊥BC于E,
∵AD∥BC,AB⊥BC,AD=4cm,BC=12cm,
∴BE=AD=4,
∴CE=BC-BE=12-4=8,
∵∠C=45°,
∴DE=CE=8<8.2,
所以乙能穿过圆洞.
故选A.
点评:考查几何图形与圆的关系;用到的知识点为:一个多边形能否穿过圆洞,只要看是否存在距离某一边所在直线最远的顶点到这条直线的距离小于圆洞的直径.

练习册系列答案
相关题目
工地上有甲、乙两块铁板,铁板甲形状为等腰三角形,其顶角为a且tana=
,腰长为10cm,铁板乙形状为直角梯形,两底边分别为4cm、10cm,且有一内角为60°,现在我们把它们任意翻转,分别试图从一个直径为8.5cm的圆洞中穿过,结果是( )
| 4 |
| 3 |
| A、甲板能穿过,乙板不能穿过 |
| B、甲板不能穿过,乙板能穿过 |
| C、甲、乙两板都能穿过 |
| D、甲、乙两板都不能穿过 |
铁板甲形状为等腰三角形,其顶角为120°,腰长16cm,铁板乙形状为直角梯形,两底分别为4cm、12cm,且有一个角为45°,现在我们把它们任意翻转,分别试图从一个直径为8.2cm的圆洞中穿过,结果( )
| A、甲、乙都能穿过 | B、甲、乙都不能穿过 | C、甲能而乙不能穿过 | D、甲不能而乙能穿过 |
工地上有甲、乙二块铁板,铁板甲形状为等腰三角形,其顶角为45º,腰长为12cm;铁板乙形状为等腰直角三角形,腰长为12cm。现在我们把它们任意翻转,分别试图从一个直径为8.5cm的圆洞中穿过,结果是( )
| A.甲板能穿过,乙板不能穿过 | B.甲板不能穿过,乙板能穿过 |
| C.甲、乙板都能穿过 | D.甲板不能穿过,乙板不能穿过 |