题目内容
4.解方程组:$\frac{3a+2b}{4}$=一$\frac{a+5b}{3}$=$\frac{2a+b+2}{5}$.分析 方程组整理后,利用加减消元法求出解即可.
解答 解:变形得:$\left\{\begin{array}{l}{\frac{3a+2b}{4}=-\frac{a+5b}{3}}\\{\frac{3a+2b}{4}=\frac{2a+b+2}{5}}\end{array}\right.$,
整理得:$\left\{\begin{array}{l}{a+2b=0①}\\{7a+6b=8②}\end{array}\right.$,
②-①×3得:4a=8,即a=2,
把a=2代入①得:b=-1,
则方程组的解为$\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
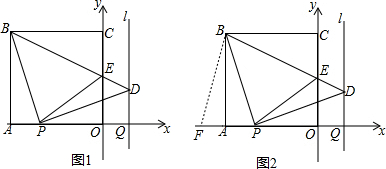
 某城市有座古塔,现要实际测量这座古塔外墙底部的底角(图中∠ABC)的大小,请运用你所学的知识设计出测量方案,并说明理由.
某城市有座古塔,现要实际测量这座古塔外墙底部的底角(图中∠ABC)的大小,请运用你所学的知识设计出测量方案,并说明理由.