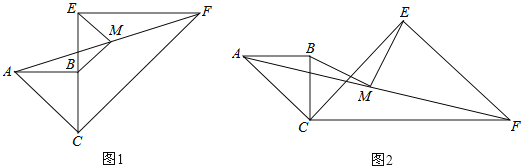
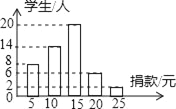
��Ŀ����
����Ŀ����ͼ���߳�Ϊ![]() ������OABC�ı�OA��OC����������.��
������OABC�ı�OA��OC����������.��![]() �����߶�
�����߶�![]() ��Q��A���ұߣ���P��A��������ÿ��1����λ���ٶ���O�˶�������P�����Oʱֹͣ�˶����˶�ʱ��Ϊ
��Q��A���ұߣ���P��A��������ÿ��1����λ���ٶ���O�˶�������P�����Oʱֹͣ�˶����˶�ʱ��Ϊ![]() .����PB����P��PB�Ĵ��ߣ���Q��
.����PB����P��PB�Ĵ��ߣ���Q��![]() ��Ĵ��ߣ��������ཻ�ڵ�D.����BD��
��Ĵ��ߣ��������ཻ�ڵ�D.����BD��![]() ���ڵ�E������PD��
���ڵ�E������PD��![]() ���ڵ�F������PE.
���ڵ�F������PE.
��1�����PBD�Ķ���.
��2�����POE���ܳ�Ϊ![]() ��̽��
��̽��![]() ��
��![]() �ĺ�����ϵʽ����д��
�ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��3����![]() ������PBEΪ����������ʱ�����EFD�����.
������PBEΪ����������ʱ�����EFD�����.
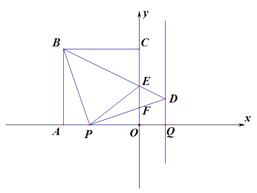
���𰸡�(1)��PBD=45�� (2) ![]() ����(3)
����(3) ![]() ��
��![]() ��
��
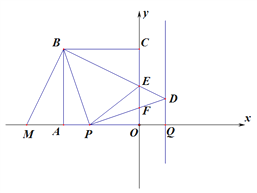
����������1����֤BAP��PQD���Ӷ��õ�DQ=AP=t���Ӷ����������PAD�Ķ���.
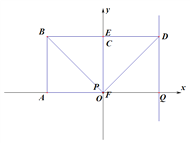
��2�����ڡ�EBP=45�㣬��ͼ1����������Ϊ������һ������ͼ�Σ�������������ȫ����l=EP+PO+EO=(CE+EO)+(AP+PO)=2AO������⣬Ȼ������������ȡ�ᣬ����ȷ��t��ȡֵ��Χֵ����3����֤��������ȫ�ȣ������EF�����ɵó������
�⣺(1) �ߡ�APB+��PBA=��APB+��DPQ=90��
���PBA=��DPQ
�֡ߡ�BAP=��PQD=90��,BA=PQ=![]()
���BAP�ա�PQD
��BP=PD
�֡�BP��PD
���PBD=45��
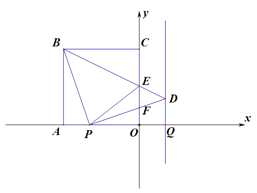
(2)�ӳ�PA��M��ʹ��AM=CE
�ڡ�BAM���BCE��
��
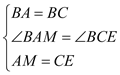
���BAM�ա�BCE
���MBA=��EBC
�ߡ�EBC+��ABP=45��
���MBP=��MBA+��ABP=45��=��EBP
�ڡ�BPM���BPE��
��
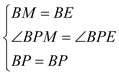
���BPM�ա�BPE
��EP=MP=MA+AP=CE+AP
�֡�l=EP+PO+EO=(CE+EO)+(AP+PO)=2AO
��![]() ����
����
(3)EP=EB
�ߡ�PBD=45��
��EP��EB ��EΪBD�е㣬
��E��C�غϣ�P��O�غ�
��ʱ��S��EFD=8����
PB=PE
�ߡ�PBD=45��
��EP��PB (������)
BP=BE
��BA=BC
���BAP�ա�BCE ��CE=AP=t![]() ��PE=2t
��PE=2t
�֡�OE=OP=![]() ��PE=
��PE=![]() ��
��![]() =
=![]() ��ã�
��ã�![]()
�ߡ�BAP�ա�PQD ��AP=QD ��D![]()
��P![]() ��
��![]()
![]() ��F
��F![]()
��EF=![]()
��ʱ��![]() ��
��
����������![]() ��
��![]() ��
��
���㾦�����⿼���������ε����ʡ����������ε����ʡ�ȫ�������ε��������ж���֪ʶ�������˷������۵�˼�룬���������û����������������������ۺ��Էdz�ǿ����Ϥ��������һ������Ϊ45��Ľ���ɵĻ���ͼ�Σ����нǵĶ����������ε�һ�������غϣ��ǵ������������ε����߷ֱ��ཻ���ǽ������Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�